Statistical and Algorithmic Insights for Semi-supervised Learning with Self-training
Paper and Code
Jun 19, 2020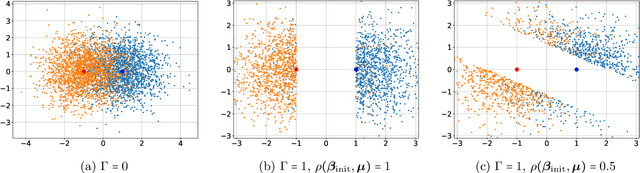
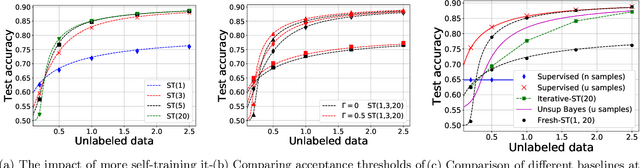
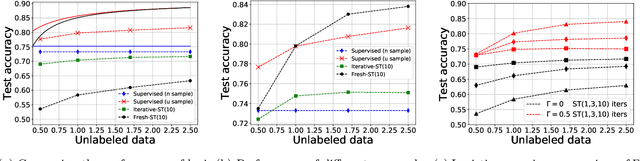
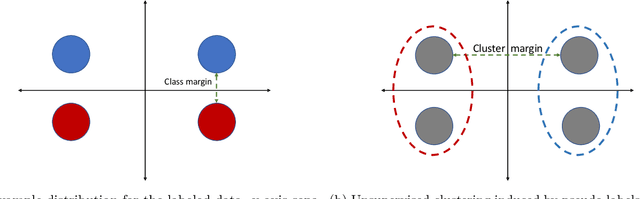
Self-training is a classical approach in semi-supervised learning which is successfully applied to a variety of machine learning problems. Self-training algorithm generates pseudo-labels for the unlabeled examples and progressively refines these pseudo-labels which hopefully coincides with the actual labels. This work provides theoretical insights into self-training algorithm with a focus on linear classifiers. We first investigate Gaussian mixture models and provide a sharp non-asymptotic finite-sample characterization of the self-training iterations. Our analysis reveals the provable benefits of rejecting samples with low confidence and demonstrates that self-training iterations gracefully improve the model accuracy even if they do get stuck in sub-optimal fixed points. We then demonstrate that regularization and class margin (i.e. separation) is provably important for the success and lack of regularization may prevent self-training from identifying the core features in the data. Finally, we discuss statistical aspects of empirical risk minimization with self-training for general distributions. We show how a purely unsupervised notion of generalization based on self-training based clustering can be formalized based on cluster margin. We then establish a connection between self-training based semi-supervision and the more general problem of learning with heterogenous data and weak supervision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge