Stronger Convergence Results for Deep Residual Networks: Network Width Scales Linearly with Training Data Size
Paper and Code
Nov 11, 2019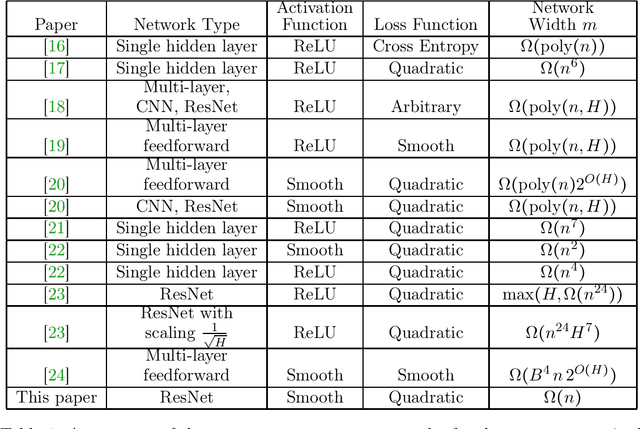
Deep neural networks are highly expressive machine learning models with the ability to interpolate arbitrary datasets. Deep nets are typically optimized via first-order methods and the optimization process crucially depends on the characteristics of the network as well as the dataset. This work sheds light on the relation between the network size and the properties of the dataset with an emphasis on deep residual networks (ResNets). Our contribution is that if the network Jacobian is full rank, gradient descent for the quadratic loss and smooth activation converges to the global minima even if the network width $m$ of the ResNet scales linearly with the sample size $n$, and independently from the network depth. To the best of our knowledge, this is the first work which provides a theoretical guarantee for the convergence of neural networks in the $m=\Omega(n)$ regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge