Long-Tailed Recognition on Binary Networks by Calibrating A Pre-trained Model

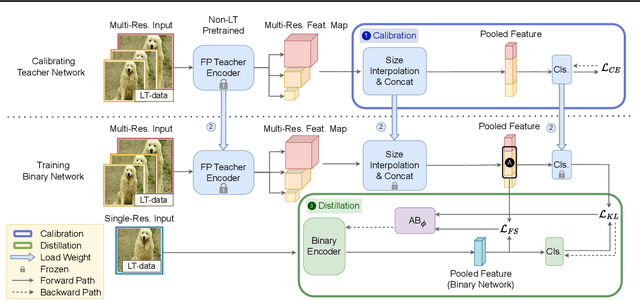
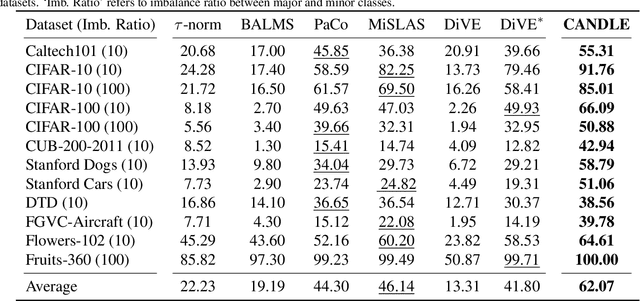
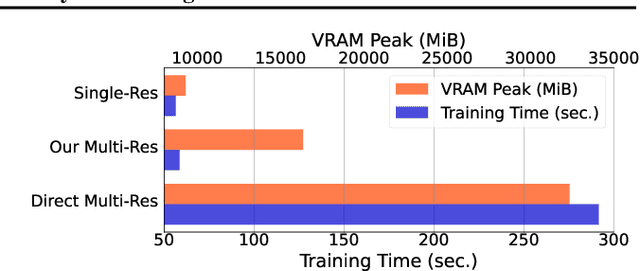
Deploying deep models in real-world scenarios entails a number of challenges, including computational efficiency and real-world (e.g., long-tailed) data distributions. We address the combined challenge of learning long-tailed distributions using highly resource-efficient binary neural networks as backbones. Specifically, we propose a calibrate-and-distill framework that uses off-the-shelf pretrained full-precision models trained on balanced datasets to use as teachers for distillation when learning binary networks on long-tailed datasets. To better generalize to various datasets, we further propose a novel adversarial balancing among the terms in the objective function and an efficient multiresolution learning scheme. We conducted the largest empirical study in the literature using 15 datasets, including newly derived long-tailed datasets from existing balanced datasets, and show that our proposed method outperforms prior art by large margins (>14.33% on average).

Inducing Point Operator Transformer: A Flexible and Scalable Architecture for Solving PDEs

Solving partial differential equations (PDEs) by learning the solution operators has emerged as an attractive alternative to traditional numerical methods. However, implementing such architectures presents two main challenges: flexibility in handling irregular and arbitrary input and output formats and scalability to large discretizations. Most existing architectures are limited by their desired structure or infeasible to scale large inputs and outputs. To address these issues, we introduce an attention-based model called an inducing-point operator transformer (IPOT). Inspired by inducing points methods, IPOT is designed to handle any input function and output query while capturing global interactions in a computationally efficient way. By detaching the inputs/outputs discretizations from the processor with a smaller latent bottleneck, IPOT offers flexibility in processing arbitrary discretizations and scales linearly with the size of inputs/outputs. Our experimental results demonstrate that IPOT achieves strong performances with manageable computational complexity on an extensive range of PDE benchmarks and real-world weather forecasting scenarios, compared to state-of-the-art methods.