UCBoost: A Boosting Approach to Tame Complexity and Optimality for Stochastic Bandits

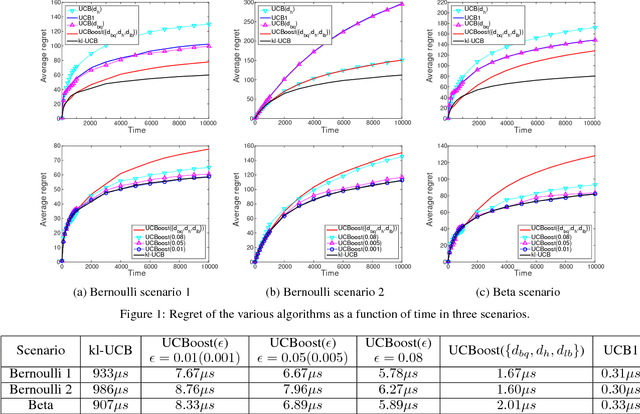
In this work, we address the open problem of finding low-complexity near-optimal multi-armed bandit algorithms for sequential decision making problems. Existing bandit algorithms are either sub-optimal and computationally simple (e.g., UCB1) or optimal and computationally complex (e.g., kl-UCB). We propose a boosting approach to Upper Confidence Bound based algorithms for stochastic bandits, that we call UCBoost. Specifically, we propose two types of UCBoost algorithms. We show that UCBoost($D$) enjoys $O(1)$ complexity for each arm per round as well as regret guarantee that is $1/e$-close to that of the kl-UCB algorithm. We propose an approximation-based UCBoost algorithm, UCBoost($\epsilon$), that enjoys a regret guarantee $\epsilon$-close to that of kl-UCB as well as $O(\log(1/\epsilon))$ complexity for each arm per round. Hence, our algorithms provide practitioners a practical way to trade optimality with computational complexity. Finally, we present numerical results which show that UCBoost($\epsilon$) can achieve the same regret performance as the standard kl-UCB while incurring only $1\%$ of the computational cost of kl-UCB.

Information Directed Sampling for Stochastic Bandits with Graph Feedback

We consider stochastic multi-armed bandit problems with graph feedback, where the decision maker is allowed to observe the neighboring actions of the chosen action. We allow the graph structure to vary with time and consider both deterministic and Erd\H{o}s-R\'enyi random graph models. For such a graph feedback model, we first present a novel analysis of Thompson sampling that leads to tighter performance bound than existing work. Next, we propose new Information Directed Sampling based policies that are graph-aware in their decision making. Under the deterministic graph case, we establish a Bayesian regret bound for the proposed policies that scales with the clique cover number of the graph instead of the number of actions. Under the random graph case, we provide a Bayesian regret bound for the proposed policies that scales with the ratio of the number of actions over the expected number of observations per iteration. To the best of our knowledge, this is the first analytical result for stochastic bandits with random graph feedback. Finally, using numerical evaluations, we demonstrate that our proposed IDS policies outperform existing approaches, including adaptions of upper confidence bound, $\epsilon$-greedy and Exp3 algorithms.

Reward Maximization Under Uncertainty: Leveraging Side-Observations on Networks

We study the stochastic multi-armed bandit (MAB) problem in the presence of side-observations across actions that occur as a result of an underlying network structure. In our model, a bipartite graph captures the relationship between actions and a common set of unknowns such that choosing an action reveals observations for the unknowns that it is connected to. This models a common scenario in online social networks where users respond to their friends' activity, thus providing side information about each other's preferences. Our contributions are as follows: 1) We derive an asymptotic lower bound (with respect to time) as a function of the bi-partite network structure on the regret of any uniformly good policy that achieves the maximum long-term average reward. 2) We propose two policies - a randomized policy; and a policy based on the well-known upper confidence bound (UCB) policies - both of which explore each action at a rate that is a function of its network position. We show, under mild assumptions, that these policies achieve the asymptotic lower bound on the regret up to a multiplicative factor, independent of the network structure. Finally, we use numerical examples on a real-world social network and a routing example network to demonstrate the benefits obtained by our policies over other existing policies.