UCBoost: A Boosting Approach to Tame Complexity and Optimality for Stochastic Bandits
Paper and Code
Apr 16, 2018
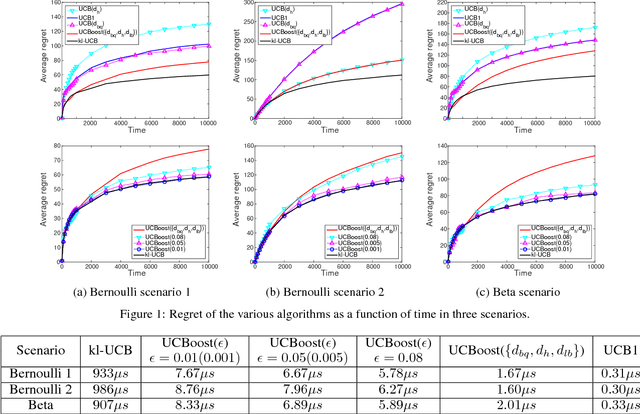
In this work, we address the open problem of finding low-complexity near-optimal multi-armed bandit algorithms for sequential decision making problems. Existing bandit algorithms are either sub-optimal and computationally simple (e.g., UCB1) or optimal and computationally complex (e.g., kl-UCB). We propose a boosting approach to Upper Confidence Bound based algorithms for stochastic bandits, that we call UCBoost. Specifically, we propose two types of UCBoost algorithms. We show that UCBoost($D$) enjoys $O(1)$ complexity for each arm per round as well as regret guarantee that is $1/e$-close to that of the kl-UCB algorithm. We propose an approximation-based UCBoost algorithm, UCBoost($\epsilon$), that enjoys a regret guarantee $\epsilon$-close to that of kl-UCB as well as $O(\log(1/\epsilon))$ complexity for each arm per round. Hence, our algorithms provide practitioners a practical way to trade optimality with computational complexity. Finally, we present numerical results which show that UCBoost($\epsilon$) can achieve the same regret performance as the standard kl-UCB while incurring only $1\%$ of the computational cost of kl-UCB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge