Suresh Nambi
ExPAN(N)D: Exploring Posits for Efficient Artificial Neural Network Design in FPGA-based Systems
Oct 27, 2020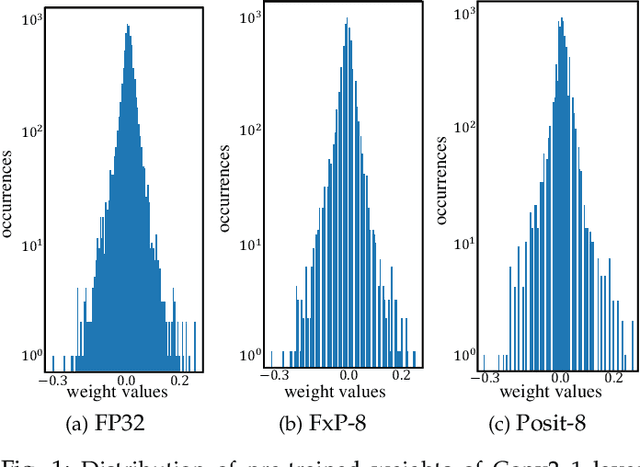
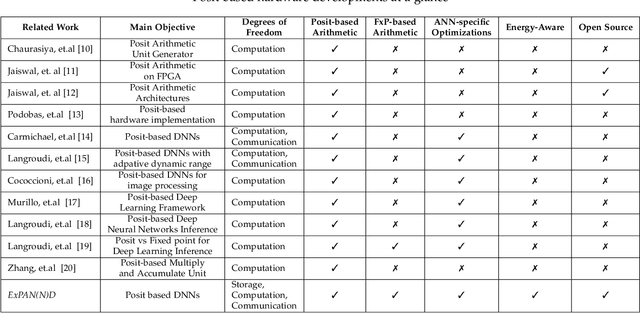
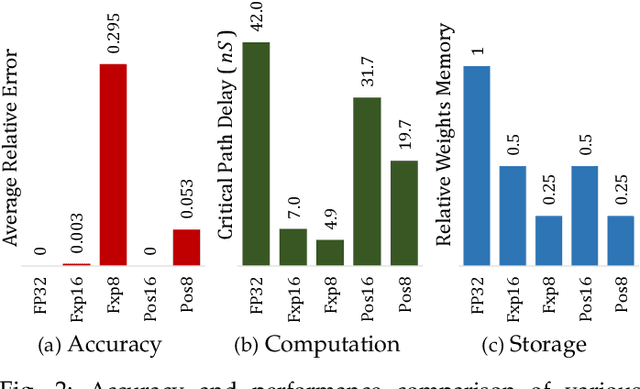
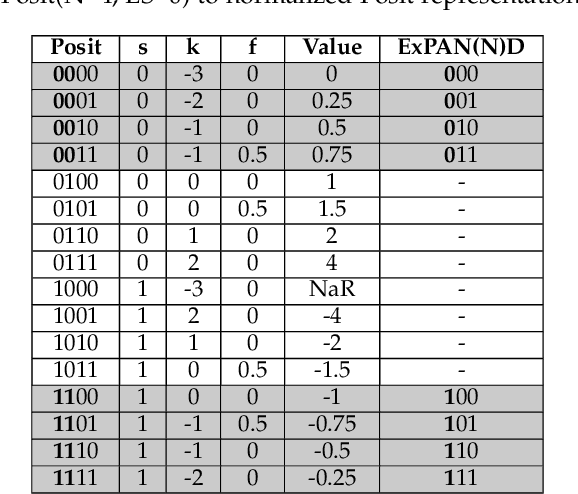
Abstract:The recent advances in machine learning, in general, and Artificial Neural Networks (ANN), in particular, has made smart embedded systems an attractive option for a larger number of application areas. However, the high computational complexity, memory footprints, and energy requirements of machine learning models hinder their deployment on resource-constrained embedded systems. Most state-of-the-art works have considered this problem by proposing various low bit-width data representation schemes, optimized arithmetic operators' implementations, and different complexity reduction techniques such as network pruning. To further elevate the implementation gains offered by these individual techniques, there is a need to cross-examine and combine these techniques' unique features. This paper presents ExPAN(N)D, a framework to analyze and ingather the efficacy of the Posit number representation scheme and the efficiency of fixed-point arithmetic implementations for ANNs. The Posit scheme offers a better dynamic range and higher precision for various applications than IEEE $754$ single-precision floating-point format. However, due to the dynamic nature of the various fields of the Posit scheme, the corresponding arithmetic circuits have higher critical path delay and resource requirements than the single-precision-based arithmetic units. Towards this end, we propose a novel Posit to fixed-point converter for enabling high-performance and energy-efficient hardware implementations for ANNs with minimal drop in the output accuracy. We also propose a modified Posit-based representation to store the trained parameters of a network. Compared to an $8$-bit fixed-point-based inference accelerator, our proposed implementation offers $\approx46\%$ and $\approx18\%$ reductions in the storage requirements of the parameters and energy consumption of the MAC units, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge