AxOMaP: Designing FPGA-based Approximate Arithmetic Operators using Mathematical Programming

With the increasing application of machine learning (ML) algorithms in embedded systems, there is a rising necessity to design low-cost computer arithmetic for these resource-constrained systems. As a result, emerging models of computation, such as approximate and stochastic computing, that leverage the inherent error-resilience of such algorithms are being actively explored for implementing ML inference on resource-constrained systems. Approximate computing (AxC) aims to provide disproportionate gains in the power, performance, and area (PPA) of an application by allowing some level of reduction in its behavioral accuracy (BEHAV). Using approximate operators (AxOs) for computer arithmetic forms one of the more prevalent methods of implementing AxC. AxOs provide the additional scope for finer granularity of optimization, compared to only precision scaling of computer arithmetic. To this end, designing platform-specific and cost-efficient approximate operators forms an important research goal. Recently, multiple works have reported using AI/ML-based approaches for synthesizing novel FPGA-based AxOs. However, most of such works limit usage of AI/ML to designing ML-based surrogate functions used during iterative optimization processes. To this end, we propose a novel data analysis-driven mathematical programming-based approach to synthesizing approximate operators for FPGAs. Specifically, we formulate mixed integer quadratically constrained programs based on the results of correlation analysis of the characterization data and use the solutions to enable a more directed search approach for evolutionary optimization algorithms. Compared to traditional evolutionary algorithms-based optimization, we report up to 21% improvement in the hypervolume, for joint optimization of PPA and BEHAV, in the design of signed 8-bit multipliers.

AxOCS: Scaling FPGA-based Approximate Operators using Configuration Supersampling

The rising usage of AI and ML-based processing across application domains has exacerbated the need for low-cost ML implementation, specifically for resource-constrained embedded systems. To this end, approximate computing, an approach that explores the power, performance, area (PPA), and behavioral accuracy (BEHAV) trade-offs, has emerged as a possible solution for implementing embedded machine learning. Due to the predominance of MAC operations in ML, designing platform-specific approximate arithmetic operators forms one of the major research problems in approximate computing. Recently there has been a rising usage of AI/ML-based design space exploration techniques for implementing approximate operators. However, most of these approaches are limited to using ML-based surrogate functions for predicting the PPA and BEHAV impact of a set of related design decisions. While this approach leverages the regression capabilities of ML methods, it does not exploit the more advanced approaches in ML. To this end, we propose AxOCS, a methodology for designing approximate arithmetic operators through ML-based supersampling. Specifically, we present a method to leverage the correlation of PPA and BEHAV metrics across operators of varying bit-widths for generating larger bit-width operators. The proposed approach involves traversing the relatively smaller design space of smaller bit-width operators and employing its associated Design-PPA-BEHAV relationship to generate initial solutions for metaheuristics-based optimization for larger operators. The experimental evaluation of AxOCS for FPGA-optimized approximate operators shows that the proposed approach significantly improves the quality-resulting hypervolume for multi-objective optimization-of 8x8 signed approximate multipliers.

ExPAN(N)D: Exploring Posits for Efficient Artificial Neural Network Design in FPGA-based Systems

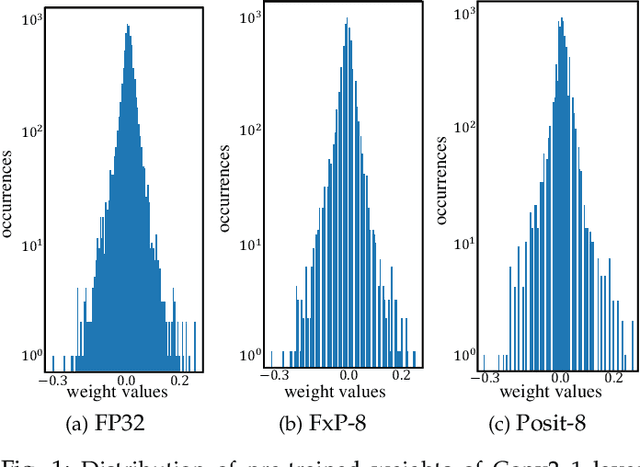
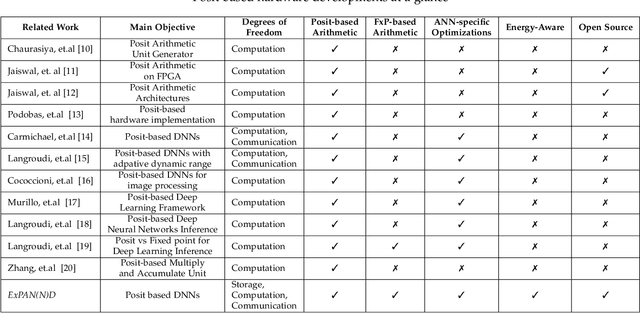
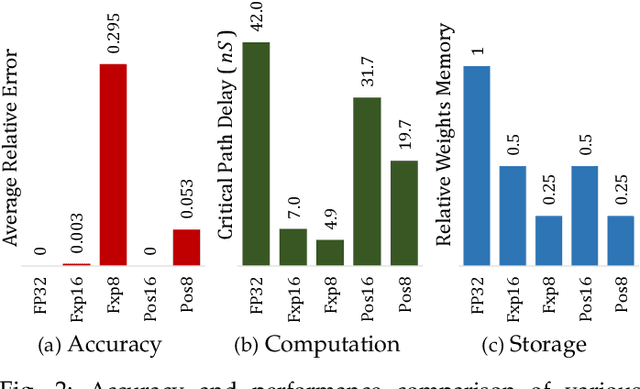
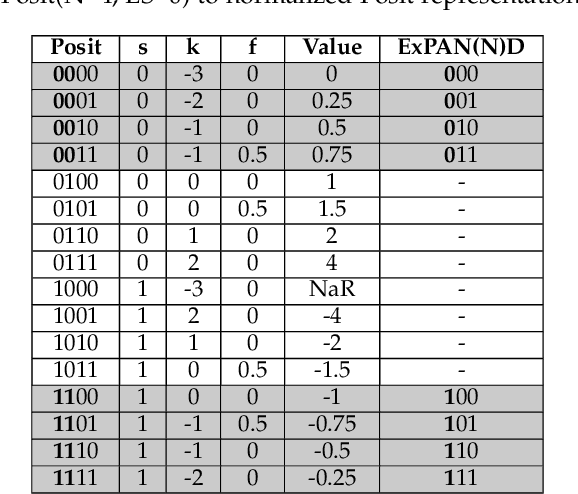
The recent advances in machine learning, in general, and Artificial Neural Networks (ANN), in particular, has made smart embedded systems an attractive option for a larger number of application areas. However, the high computational complexity, memory footprints, and energy requirements of machine learning models hinder their deployment on resource-constrained embedded systems. Most state-of-the-art works have considered this problem by proposing various low bit-width data representation schemes, optimized arithmetic operators' implementations, and different complexity reduction techniques such as network pruning. To further elevate the implementation gains offered by these individual techniques, there is a need to cross-examine and combine these techniques' unique features. This paper presents ExPAN(N)D, a framework to analyze and ingather the efficacy of the Posit number representation scheme and the efficiency of fixed-point arithmetic implementations for ANNs. The Posit scheme offers a better dynamic range and higher precision for various applications than IEEE $754$ single-precision floating-point format. However, due to the dynamic nature of the various fields of the Posit scheme, the corresponding arithmetic circuits have higher critical path delay and resource requirements than the single-precision-based arithmetic units. Towards this end, we propose a novel Posit to fixed-point converter for enabling high-performance and energy-efficient hardware implementations for ANNs with minimal drop in the output accuracy. We also propose a modified Posit-based representation to store the trained parameters of a network. Compared to an $8$-bit fixed-point-based inference accelerator, our proposed implementation offers $\approx46\%$ and $\approx18\%$ reductions in the storage requirements of the parameters and energy consumption of the MAC units, respectively.