Model-based free-breathing cardiac MRI reconstruction using deep learned \& STORM priors: MoDL-STORM

We introduce a model-based reconstruction framework with deep learned (DL) and smoothness regularization on manifolds (STORM) priors to recover free breathing and ungated (FBU) cardiac MRI from highly undersampled measurements. The DL priors enable us to exploit the local correlations, while the STORM prior enables us to make use of the extensive non-local similarities that are subject dependent. We introduce a novel model-based formulation that allows the seamless integration of deep learning methods with available prior information, which current deep learning algorithms are not capable of. The experimental results demonstrate the preliminary potential of this work in accelerating FBU cardiac MRI.

Recovery of Noisy Points on Band-limited Surfaces: Kernel Methods Re-explained

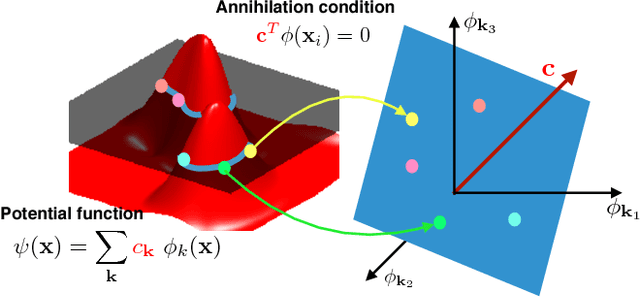
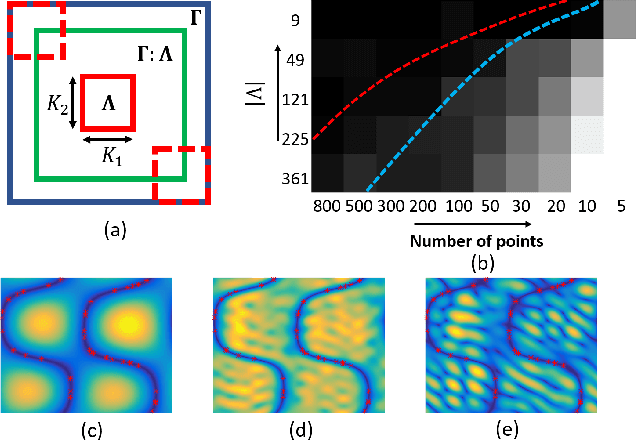
We introduce a continuous domain framework for the recovery of points on a surface in high dimensional space, represented as the zero-level set of a bandlimited function. We show that the exponential maps of the points on the surface satisfy annihilation relations, implying that they lie in a finite dimensional subspace. The subspace properties are used to derive sampling conditions, which will guarantee the perfect recovery of the surface from finite number of points. We rely on nuclear norm minimization to exploit the low-rank structure of the maps to recover the points from noisy measurements. Since the direct estimation of the surface is computationally prohibitive in very high dimensions, we propose an iterative reweighted algorithm using the "kernel trick". The iterative algorithm reveals deep links to Laplacian based algorithms widely used in graph signal processing; the theory and the sampling conditions can serve as a basis for discrete-continuous domain processing of signals on a graph.

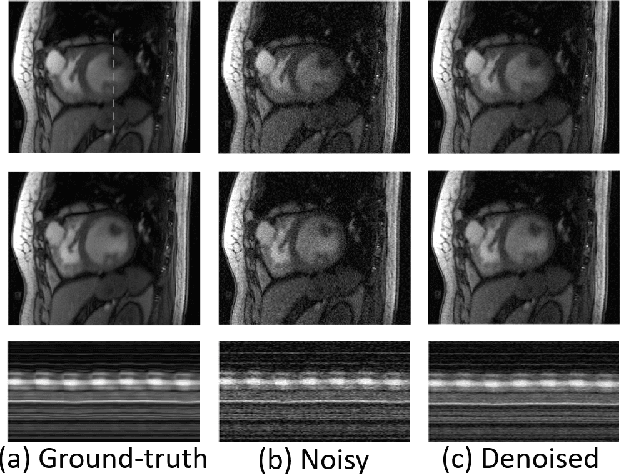
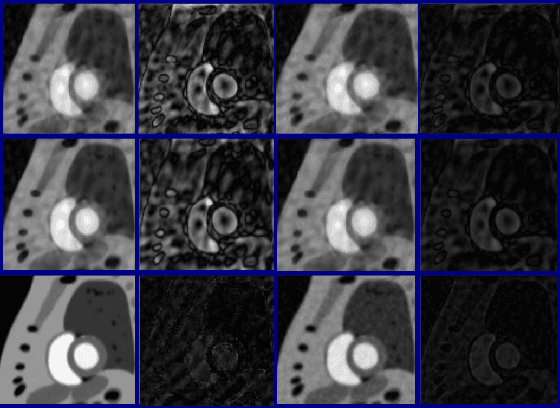
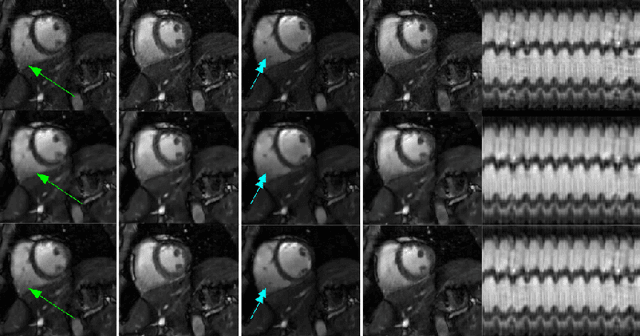
Free-breathing cardiac MRI using bandlimited manifold modelling

We introduce a novel bandlimited manifold framework and an algorithm to recover freebreathing and ungated cardiac MR images from highly undersampled measurements. The image frames in the free breathing and ungated dataset are assumed to be points on a bandlimited manifold. We introduce a novel kernel low-rank algorithm to estimate the manifold structure (Laplacian) from a navigator-based acquisition scheme. The structure of the manifold is then used to recover the images from highly undersampled measurements. A computationally efficient algorithm, which relies on the bandlimited approximation of the Laplacian matrix, is used to recover the images. The proposed scheme is demonstrated on several patients with different breathing patterns and cardiac rates, without requiring the need for manually tuning the reconstruction parameters in each case. The proposed scheme enabled the recovery of free-breathing and ungated data, providing reconstructions that are qualitatively similar to breath-held scans performed on the same patients. This shows the potential of the technique as a clinical protocol for free-breathing cardiac scans.

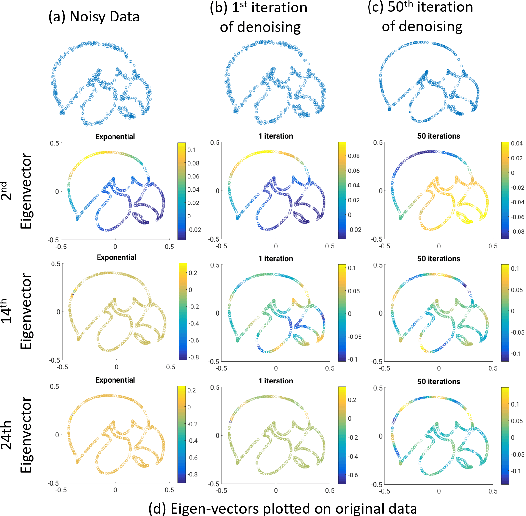
Clustering of Data with Missing Entries

The analysis of large datasets is often complicated by the presence of missing entries, mainly because most of the current machine learning algorithms are designed to work with full data. The main focus of this work is to introduce a clustering algorithm, that will provide good clustering even in the presence of missing data. The proposed technique solves an $\ell_0$ fusion penalty based optimization problem to recover the clusters. We theoretically analyze the conditions needed for the successful recovery of the clusters. We also propose an algorithm to solve a relaxation of this problem using saturating non-convex fusion penalties. The method is demonstrated on simulated and real datasets, and is observed to perform well in the presence of large fractions of missing entries.

Recovery of Point Clouds on Surfaces: Application to Image Reconstruction

We introduce a framework for the recovery of points on a smooth surface in high-dimensional space, with application to dynamic imaging. We assume the surface to be the zero-level set of a bandlimited function. We show that the exponential maps of the points on the surface satisfy annihilation relations, implying that they lie in a finite dimensional subspace. We rely on nuclear norm minimization of the maps to recover the points from noisy and undersampled measurements. Since this direct approach suffers from the curse of dimensionality, we introduce an iterative reweighted algorithm that uses the "kernel trick". The resulting algorithm has similarities to iterative algorithms used in graph signal processing (GSP); this framework can be seen as a continuous domain alternative to discrete GSP theory. The use of the algorithm in recovering free breathing and ungated cardiac data shows the potential of this framework in practical applications.

Clustering of Data with Missing Entries using Non-convex Fusion Penalties

The presence of missing entries in data often creates challenges for pattern recognition algorithms. Traditional algorithms for clustering data assume that all the feature values are known for every data point. We propose a method to cluster data in the presence of missing information. Unlike conventional clustering techniques where every feature is known for each point, our algorithm can handle cases where a few feature values are unknown for every point. For this more challenging problem, we provide theoretical guarantees for clustering using a $\ell_0$ fusion penalty based optimization problem. Furthermore, we propose an algorithm to solve a relaxation of this problem using saturating non-convex fusion penalties. It is observed that this algorithm produces solutions that degrade gradually with an increase in the fraction of missing feature values. We demonstrate the utility of the proposed method using a simulated dataset, the Wine dataset and also an under-sampled cardiac MRI dataset. It is shown that the proposed method is a promising clustering technique for datasets with large fractions of missing entries.

Two step recovery of jointly sparse and low-rank matrices: theoretical guarantees

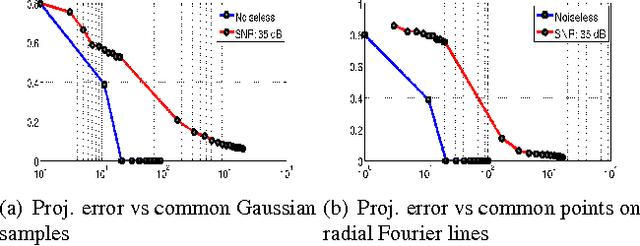
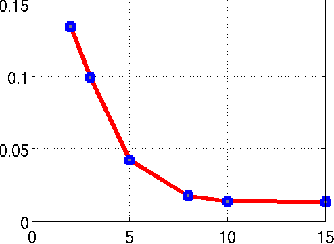
We introduce a two step algorithm with theoretical guarantees to recover a jointly sparse and low-rank matrix from undersampled measurements of its columns. The algorithm first estimates the row subspace of the matrix using a set of common measurements of the columns. In the second step, the subspace aware recovery of the matrix is solved using a simple least square algorithm. The results are verified in the context of recovering CINE data from undersampled measurements; we obtain good recovery when the sampling conditions are satisfied.

Subspace based low rank and joint sparse matrix recovery

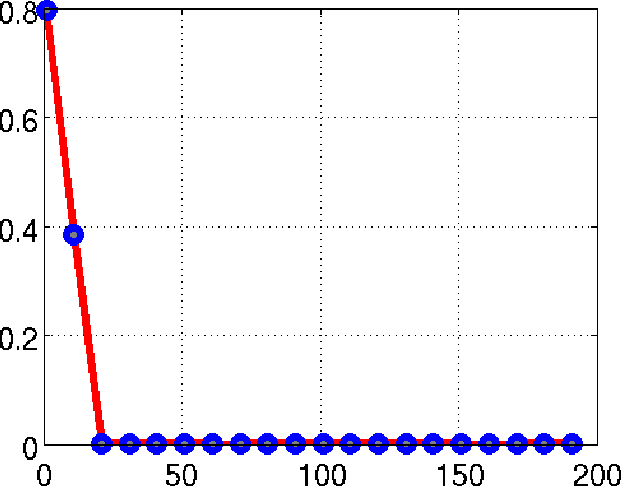
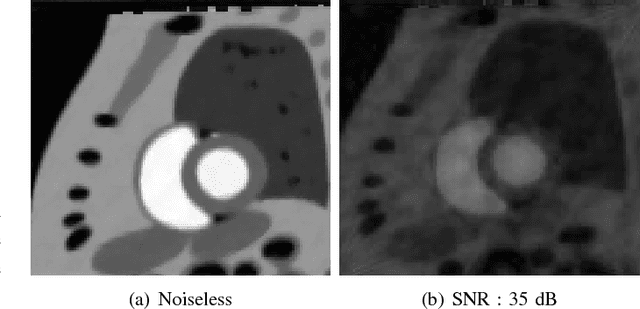
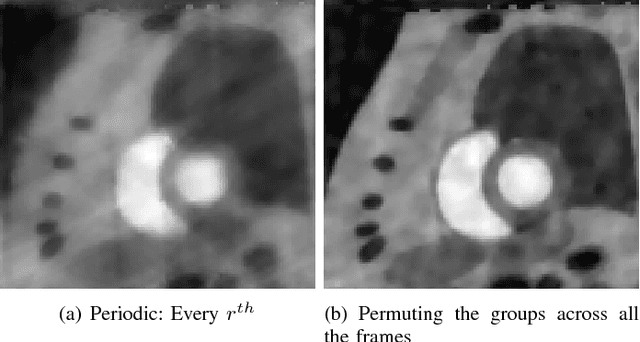
We consider the recovery of a low rank and jointly sparse matrix from under sampled measurements of its columns. This problem is highly relevant in the recovery of dynamic MRI data with high spatio-temporal resolution, where each column of the matrix corresponds to a frame in the image time series; the matrix is highly low-rank since the frames are highly correlated. Similarly the non-zero locations of the matrix in appropriate transform/frame domains (e.g. wavelet, gradient) are roughly the same in different frame. The superset of the support can be safely assumed to be jointly sparse. Unlike the classical multiple measurement vector (MMV) setup that measures all the snapshots using the same matrix, we consider each snapshot to be measured using a different measurement matrix. We show that this approach reduces the total number of measurements, especially when the rank of the matrix is much smaller than than its sparsity. Our experiments in the context of dynamic imaging shows that this approach is very useful in realizing free breathing cardiac MRI.