Recovery of Noisy Points on Band-limited Surfaces: Kernel Methods Re-explained
Paper and Code
Mar 19, 2018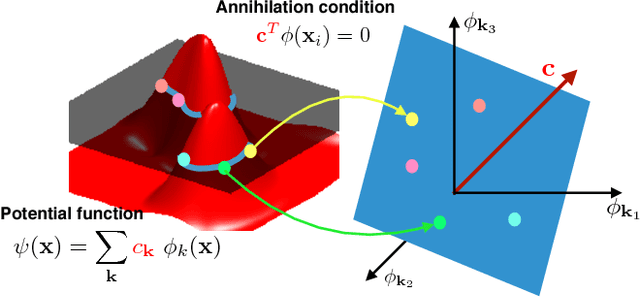
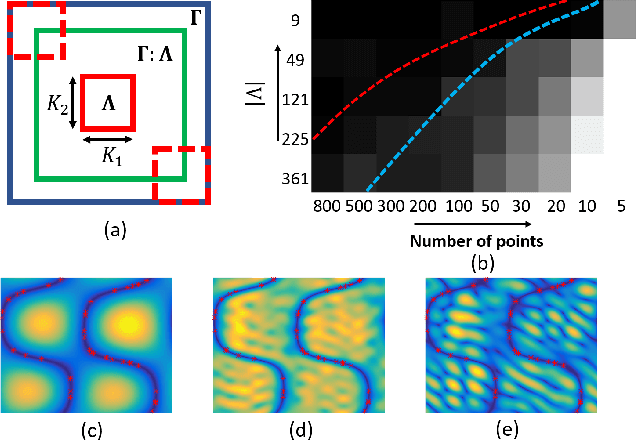
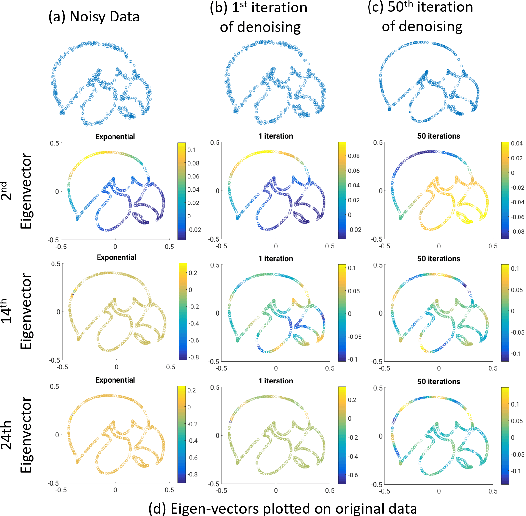
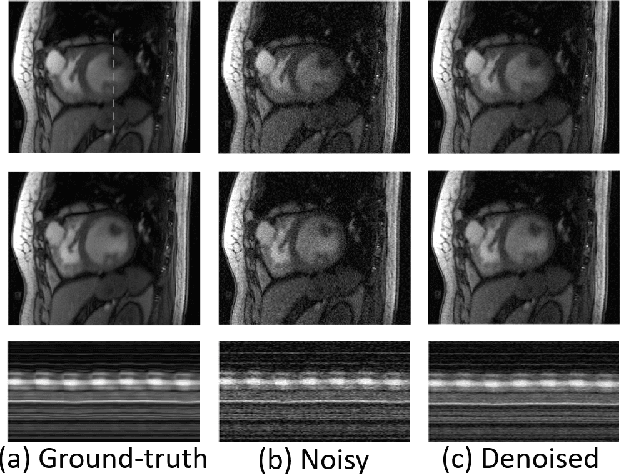
We introduce a continuous domain framework for the recovery of points on a surface in high dimensional space, represented as the zero-level set of a bandlimited function. We show that the exponential maps of the points on the surface satisfy annihilation relations, implying that they lie in a finite dimensional subspace. The subspace properties are used to derive sampling conditions, which will guarantee the perfect recovery of the surface from finite number of points. We rely on nuclear norm minimization to exploit the low-rank structure of the maps to recover the points from noisy measurements. Since the direct estimation of the surface is computationally prohibitive in very high dimensions, we propose an iterative reweighted algorithm using the "kernel trick". The iterative algorithm reveals deep links to Laplacian based algorithms widely used in graph signal processing; the theory and the sampling conditions can serve as a basis for discrete-continuous domain processing of signals on a graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge