Subspace based low rank and joint sparse matrix recovery

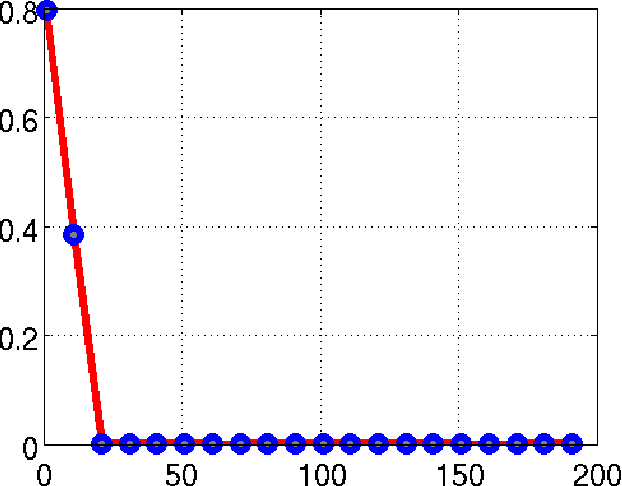
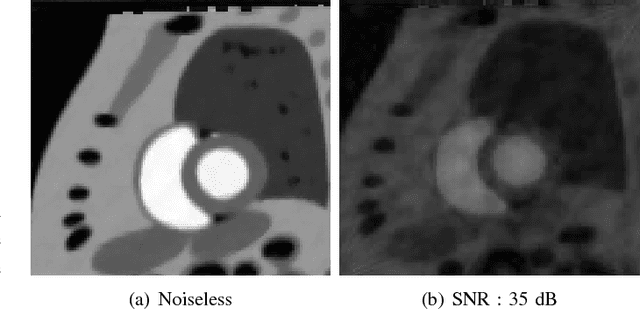
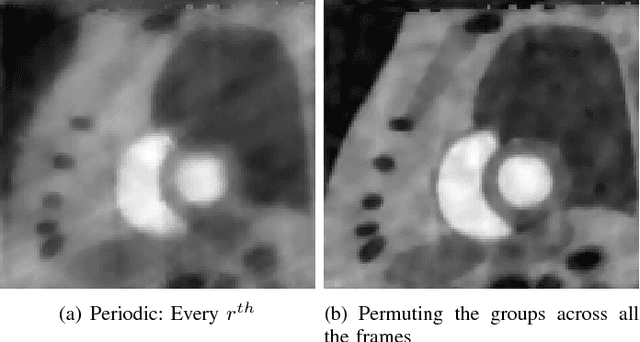
We consider the recovery of a low rank and jointly sparse matrix from under sampled measurements of its columns. This problem is highly relevant in the recovery of dynamic MRI data with high spatio-temporal resolution, where each column of the matrix corresponds to a frame in the image time series; the matrix is highly low-rank since the frames are highly correlated. Similarly the non-zero locations of the matrix in appropriate transform/frame domains (e.g. wavelet, gradient) are roughly the same in different frame. The superset of the support can be safely assumed to be jointly sparse. Unlike the classical multiple measurement vector (MMV) setup that measures all the snapshots using the same matrix, we consider each snapshot to be measured using a different measurement matrix. We show that this approach reduces the total number of measurements, especially when the rank of the matrix is much smaller than than its sparsity. Our experiments in the context of dynamic imaging shows that this approach is very useful in realizing free breathing cardiac MRI.