Model-based free-breathing cardiac MRI reconstruction using deep learned \& STORM priors: MoDL-STORM

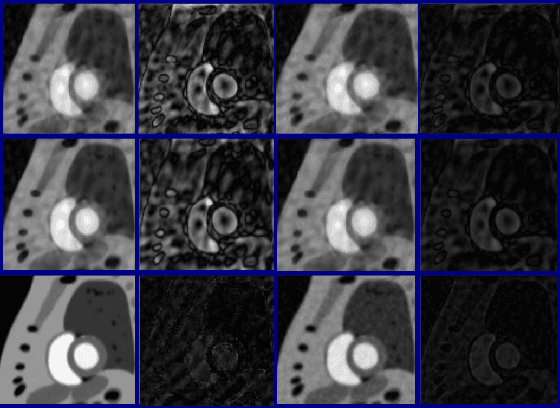
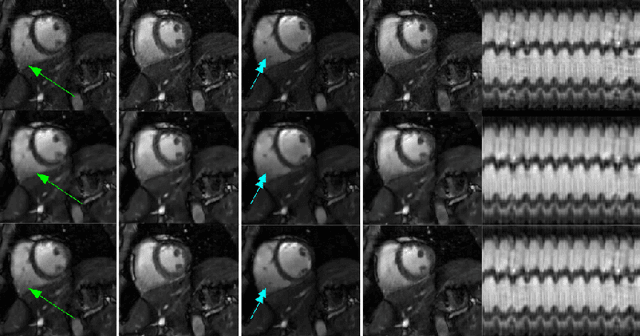
We introduce a model-based reconstruction framework with deep learned (DL) and smoothness regularization on manifolds (STORM) priors to recover free breathing and ungated (FBU) cardiac MRI from highly undersampled measurements. The DL priors enable us to exploit the local correlations, while the STORM prior enables us to make use of the extensive non-local similarities that are subject dependent. We introduce a novel model-based formulation that allows the seamless integration of deep learning methods with available prior information, which current deep learning algorithms are not capable of. The experimental results demonstrate the preliminary potential of this work in accelerating FBU cardiac MRI.

Two step recovery of jointly sparse and low-rank matrices: theoretical guarantees

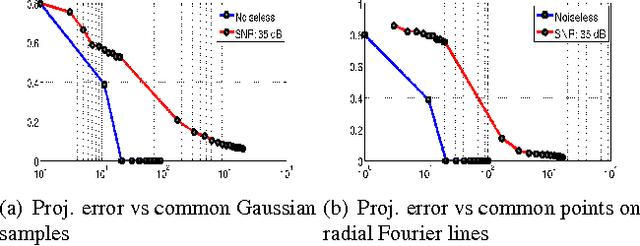
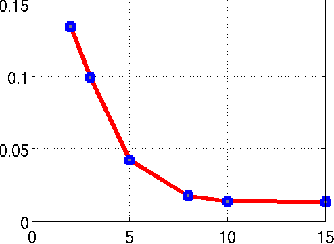
We introduce a two step algorithm with theoretical guarantees to recover a jointly sparse and low-rank matrix from undersampled measurements of its columns. The algorithm first estimates the row subspace of the matrix using a set of common measurements of the columns. In the second step, the subspace aware recovery of the matrix is solved using a simple least square algorithm. The results are verified in the context of recovering CINE data from undersampled measurements; we obtain good recovery when the sampling conditions are satisfied.

Subspace based low rank and joint sparse matrix recovery

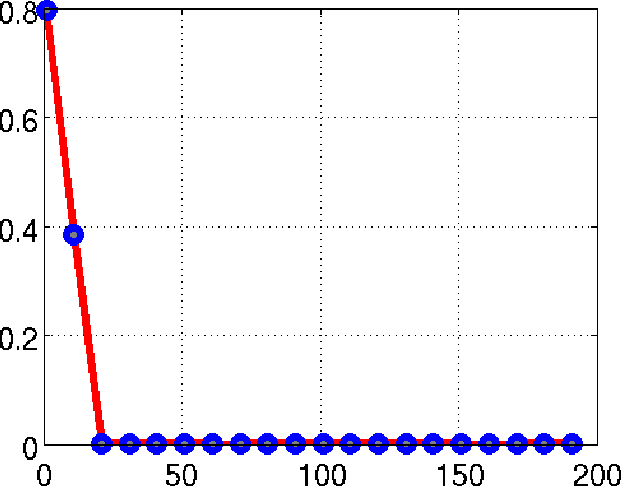
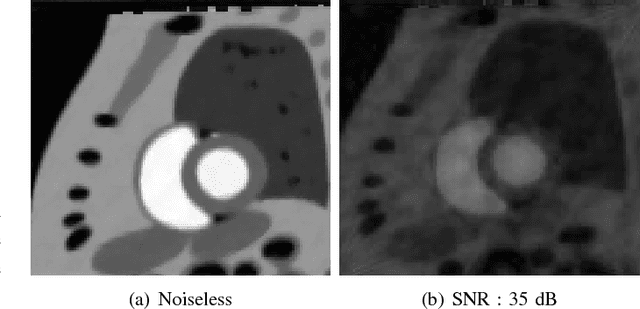
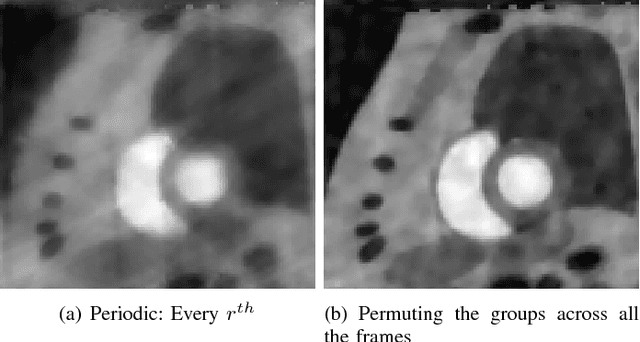
We consider the recovery of a low rank and jointly sparse matrix from under sampled measurements of its columns. This problem is highly relevant in the recovery of dynamic MRI data with high spatio-temporal resolution, where each column of the matrix corresponds to a frame in the image time series; the matrix is highly low-rank since the frames are highly correlated. Similarly the non-zero locations of the matrix in appropriate transform/frame domains (e.g. wavelet, gradient) are roughly the same in different frame. The superset of the support can be safely assumed to be jointly sparse. Unlike the classical multiple measurement vector (MMV) setup that measures all the snapshots using the same matrix, we consider each snapshot to be measured using a different measurement matrix. We show that this approach reduces the total number of measurements, especially when the rank of the matrix is much smaller than than its sparsity. Our experiments in the context of dynamic imaging shows that this approach is very useful in realizing free breathing cardiac MRI.