Sunho Park
Bayesian Semi-nonnegative Tri-matrix Factorization to Identify Pathways Associated with Cancer Types
Dec 01, 2017
Abstract:Identifying altered pathways that are associated with specific cancer types can potentially bring a significant impact on cancer patient treatment. Accurate identification of such key altered pathways information can be used to develop novel therapeutic agents as well as to understand the molecular mechanisms of various types of cancers better. Tri-matrix factorization is an efficient tool to learn associations between two different entities (e.g., cancer types and pathways in our case) from data. To successfully apply tri-matrix factorization methods to biomedical problems, biological prior knowledge such as pathway databases or protein-protein interaction (PPI) networks, should be taken into account in the factorization model. However, it is not straightforward in the Bayesian setting even though Bayesian methods are more appealing than point estimate methods, such as a maximum likelihood or a maximum posterior method, in the sense that they calculate distributions over variables and are robust against overfitting. We propose a Bayesian (semi-)nonnegative matrix factorization model for human cancer genomic data, where the biological prior knowledge represented by a pathway database and a PPI network is taken into account in the factorization model through a finite dependent Beta-Bernoulli prior. We tested our method on The Cancer Genome Atlas (TCGA) dataset and found that the pathways identified by our method can be used as a prognostic biomarkers for patient subgroup identification.
Convex Optimization for Binary Classifier Aggregation in Multiclass Problems
Jan 16, 2014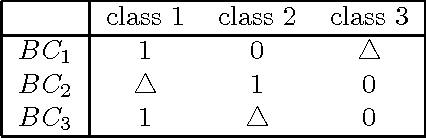
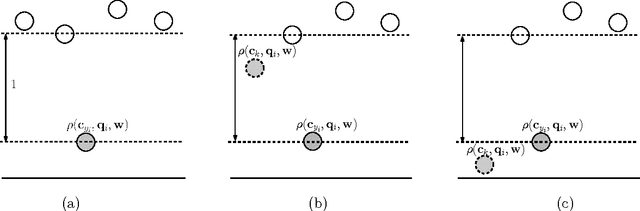
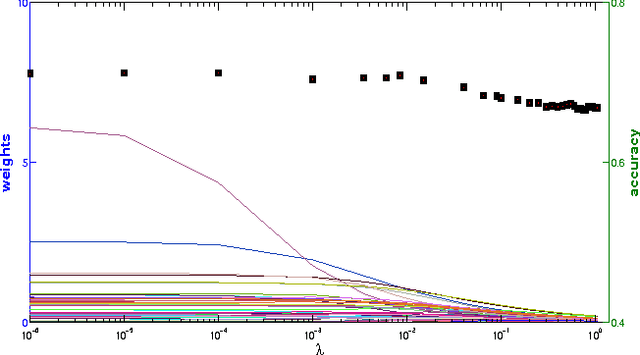
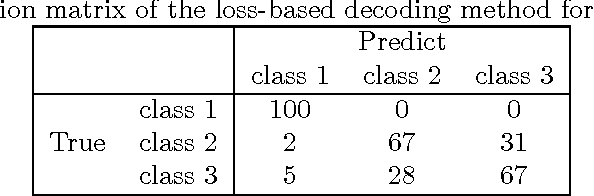
Abstract:Multiclass problems are often decomposed into multiple binary problems that are solved by individual binary classifiers whose results are integrated into a final answer. Various methods, including all-pairs (APs), one-versus-all (OVA), and error correcting output code (ECOC), have been studied, to decompose multiclass problems into binary problems. However, little study has been made to optimally aggregate binary problems to determine a final answer to the multiclass problem. In this paper we present a convex optimization method for an optimal aggregation of binary classifiers to estimate class membership probabilities in multiclass problems. We model the class membership probability as a softmax function which takes a conic combination of discrepancies induced by individual binary classifiers, as an input. With this model, we formulate the regularized maximum likelihood estimation as a convex optimization problem, which is solved by the primal-dual interior point method. Connections of our method to large margin classifiers are presented, showing that the large margin formulation can be considered as a limiting case of our convex formulation. Numerical experiments on synthetic and real-world data sets demonstrate that our method outperforms existing aggregation methods as well as direct methods, in terms of the classification accuracy and the quality of class membership probability estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge