Convex Optimization for Binary Classifier Aggregation in Multiclass Problems
Paper and Code
Jan 16, 2014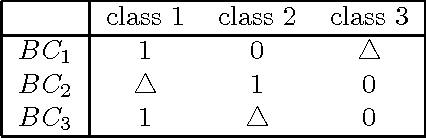
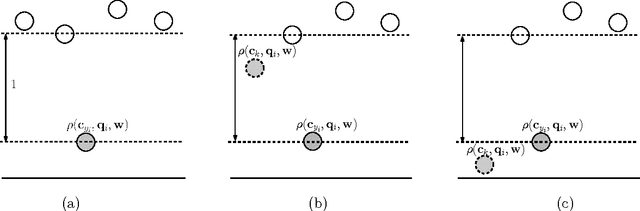
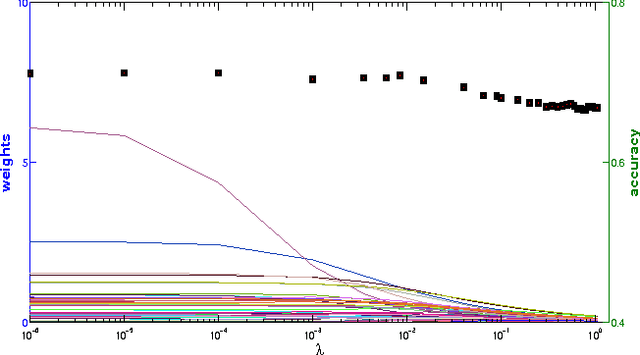
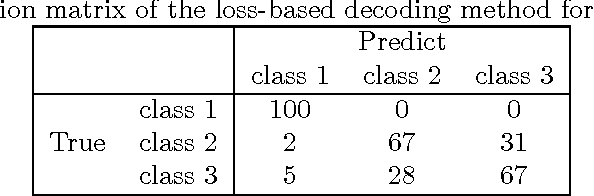
Multiclass problems are often decomposed into multiple binary problems that are solved by individual binary classifiers whose results are integrated into a final answer. Various methods, including all-pairs (APs), one-versus-all (OVA), and error correcting output code (ECOC), have been studied, to decompose multiclass problems into binary problems. However, little study has been made to optimally aggregate binary problems to determine a final answer to the multiclass problem. In this paper we present a convex optimization method for an optimal aggregation of binary classifiers to estimate class membership probabilities in multiclass problems. We model the class membership probability as a softmax function which takes a conic combination of discrepancies induced by individual binary classifiers, as an input. With this model, we formulate the regularized maximum likelihood estimation as a convex optimization problem, which is solved by the primal-dual interior point method. Connections of our method to large margin classifiers are presented, showing that the large margin formulation can be considered as a limiting case of our convex formulation. Numerical experiments on synthetic and real-world data sets demonstrate that our method outperforms existing aggregation methods as well as direct methods, in terms of the classification accuracy and the quality of class membership probability estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge