Forecasting VIX using interpretable Kolmogorov-Arnold networks

This paper presents the use of Kolmogorov-Arnold Networks (KANs) for forecasting the CBOE Volatility Index (VIX). Unlike traditional MLP-based neural networks that are often criticized for their black-box nature, KAN offers an interpretable approach via learnable spline-based activation functions and symbolification. Based on a parsimonious architecture with symbolic functions, KAN expresses a forecast of the VIX as a closed-form in terms of explanatory variables, and provide interpretable insights into key characteristics of the VIX, including mean reversion and the leverage effect. Through in-depth empirical analysis across multiple datasets and periods, we show that KANs achieve competitive forecasting performance while requiring significantly fewer parameters compared to MLP-based neural network models. Our findings demonstrate the capacity and potential of KAN as an interpretable financial time-series forecasting method.

Deep learning for undersampled MRI reconstruction

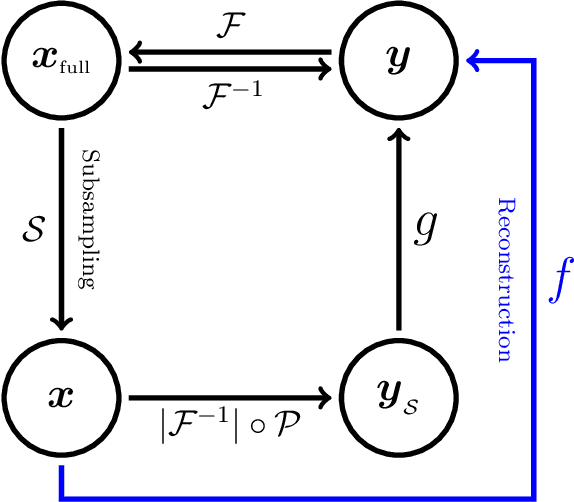
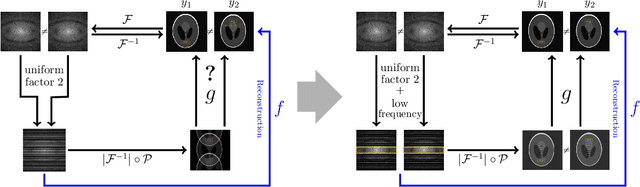
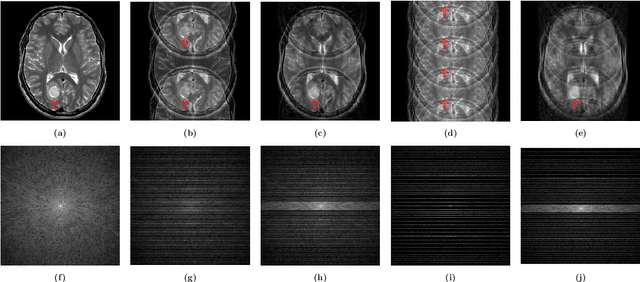
This paper presents a deep learning method for faster magnetic resonance imaging (MRI) by reducing k-space data with sub-Nyquist sampling strategies and provides a rationale for why the proposed approach works well. Uniform subsampling is used in the time-consuming phase-encoding direction to capture high-resolution image information, while permitting the image-folding problem dictated by the Poisson summation formula. To deal with the localization uncertainty due to image folding, very few low-frequency k-space data are added. Training the deep learning net involves input and output images that are pairs of Fourier transforms of the subsampled and fully sampled k-space data. Numerous experiments show the remarkable performance of the proposed method; only 29% of k-space data can generate images of high quality as effectively as standard MRI reconstruction with fully sampled data.