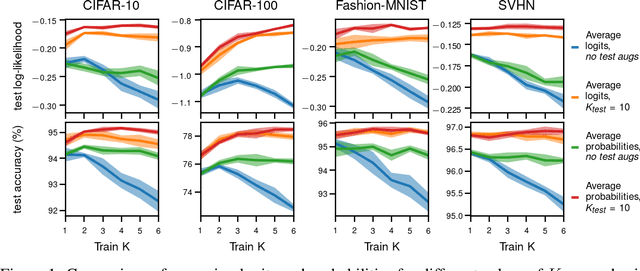
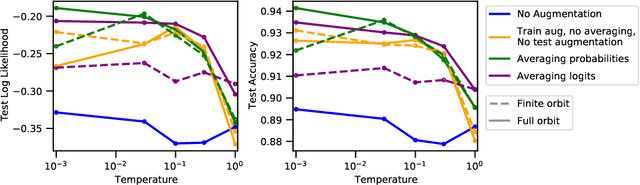
Data augmentation in Bayesian neural networks and the cold posterior effect

Data augmentation is a highly effective approach for improving performance in deep neural networks. The standard view is that it creates an enlarged dataset by adding synthetic data, which raises a problem when combining it with Bayesian inference: how much data are we really conditioning on? This question is particularly relevant to recent observations linking data augmentation to the cold posterior effect. We investigate various principled ways of finding a log-likelihood for augmented datasets. Our approach prescribes augmenting the same underlying image multiple times, both at test and train-time, and averaging either the logits or the predictive probabilities. Empirically, we observe the best performance with averaging probabilities. While there are interactions with the cold posterior effect, neither averaging logits or averaging probabilities eliminates it.