Practical application improvement to Quantum SVM: theory to practice

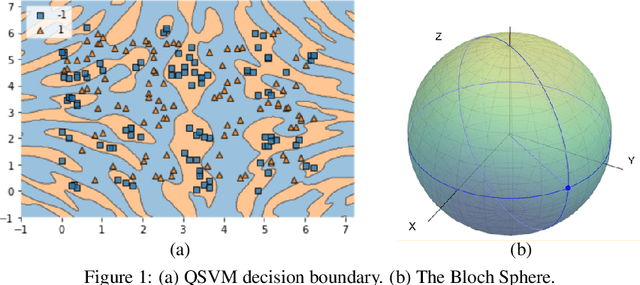
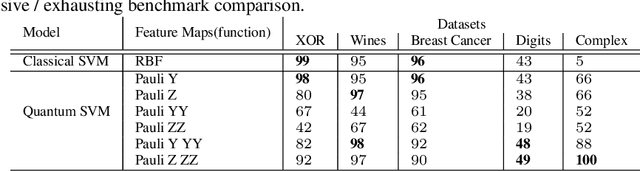
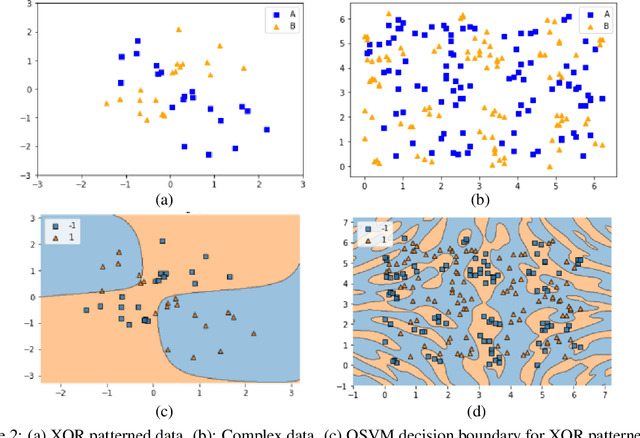
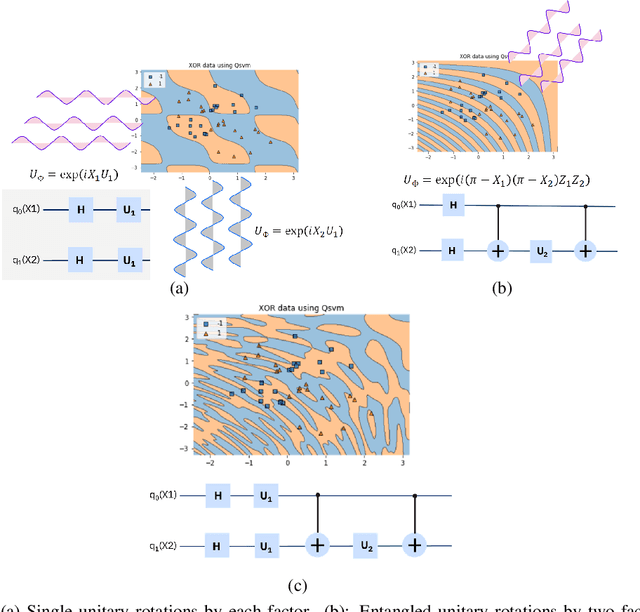
Quantum machine learning (QML) has emerged as an important area for Quantum applications, although useful QML applications would require many qubits. Therefore our paper is aimed at exploring the successful application of the Quantum Support Vector Machine (QSVM) algorithm while balancing several practical and technical considerations under the Noisy Intermediate-Scale Quantum (NISQ) assumption. For the quantum SVM under NISQ, we use quantum feature maps to translate data into quantum states and build the SVM kernel out of these quantum states, and further compare with classical SVM with radial basis function (RBF) kernels. As data sets are more complex or abstracted in some sense, classical SVM with classical kernels leads to less accuracy compared to QSVM, as classical SVM with typical classical kernels cannot easily separate different class data. Similarly, QSVM should be able to provide competitive performance over a broader range of data sets including ``simpler'' data cases in which smoother decision boundaries are required to avoid any model variance issues (i.e., overfitting). To bridge the gap between ``classical-looking'' decision boundaries and complex quantum decision boundaries, we propose to utilize general shallow unitary transformations to create feature maps with rotation factors to define a tunable quantum kernel, and added regularization to smooth the separating hyperplane model. We show in experiments that this allows QSVM to perform equally to SVM regardless of the complexity of the data sets and outperform in some commonly used reference data sets.

A Domain-agnostic, Noise-resistant, Hardware-efficient Evolutionary Variational Quantum Eigensolver

Variational quantum algorithms have shown promise in numerous fields due to their versatility in solving problems of scientific and commercial interest. However, leading algorithms for Hamiltonian simulation, such as the Variational Quantum Eigensolver (VQE), use fixed preconstructed ansatzes, limiting their general applicability and accuracy. Thus, variational forms---the quantum circuits that implement ansatzes ---are either crafted heuristically or by encoding domain-specific knowledge. In this paper, we present an Evolutionary Variational Quantum Eigensolver (EVQE), a novel variational algorithm that uses evolutionary programming techniques to minimize the expectation value of a given Hamiltonian by dynamically generating and optimizing an ansatz. The algorithm is equally applicable to optimization problems in all domains, obtaining accurate energy evaluations with hardware-efficient ansatzes. In molecular simulations, the variational forms generated by EVQE are up to $18.6\times$ shallower and use up to $12\times$ fewer CX gates than those obtained by VQE with a unitary coupled cluster ansatz. EVQE demonstrates significant noise-resistance properties, obtaining results in noisy simulation with at least $3.6\times$ less error than VQE using any tested ansatz configuration. We successfully evaluated EVQE on a real 5-qubit IBMQ quantum computer. The experimental results, which we obtained both via simulation and on real quantum hardware, demonstrate the effectiveness of EVQE for general-purpose optimization on the quantum computers of the present and near future.