retina-VAE: Variationally Decoding the Spectrum of Macular Disease

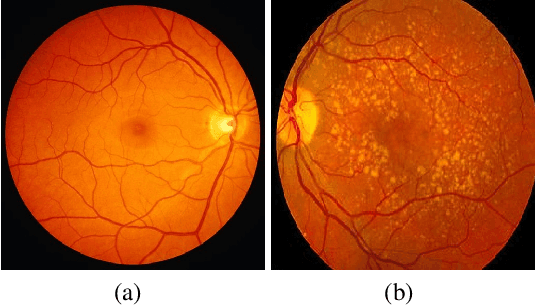
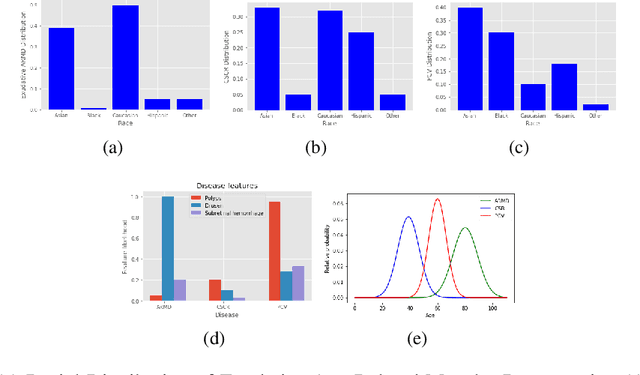
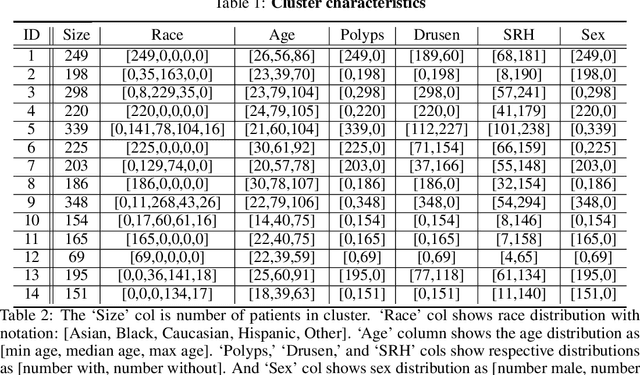
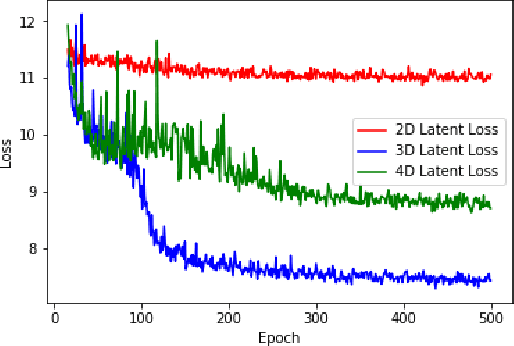
In this paper, we seek a clinically-relevant latent code for representing the spectrum of macular disease. Towards this end, we construct retina-VAE, a variational autoencoder-based model that accepts a patient profile vector (pVec) as input. The pVec components include clinical exam findings and demographic information. We evaluate the model on a subspectrum of the retinal maculopathies, in particular, exudative age-related macular degeneration, central serous chorioretinopathy, and polypoidal choroidal vasculopathy. For these three maculopathies, a database of 3000 6-dimensional pVecs (1000 each) was synthetically generated based on known disease statistics in the literature. The database was then used to train the VAE and generate latent vector representations. We found training performance to be best for a 3-dimensional latent vector architecture compared to 2 or 4 dimensional latents. Additionally, for the 3D latent architecture, we discovered that the resulting latent vectors were strongly clustered spontaneously into one of 14 clusters. Kmeans was then used only to identify members of each cluster and to inspect cluster properties. These clusters suggest underlying disease subtypes which may potentially respond better or worse to particular pharmaceutical treatments such as anti-vascular endothelial growth factor variants. The retina-VAE framework will potentially yield new fundamental insights into the mechanisms and manifestations of disease. And will potentially facilitate the development of personalized pharmaceuticals and gene therapies.

Is 'Unsupervised Learning' a Misconceived Term?

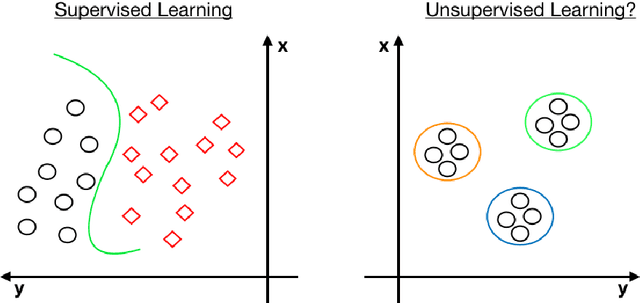
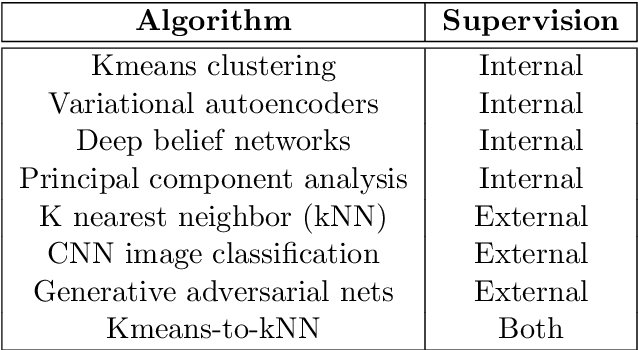
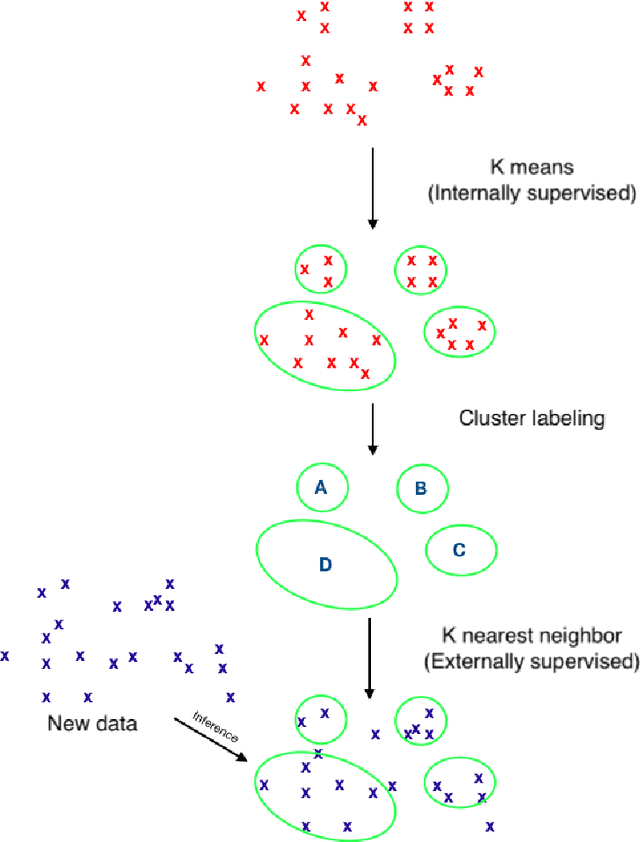
Is all of machine learning supervised to some degree? The field of machine learning has traditionally been categorized pedagogically into $supervised~vs~unsupervised~learning$; where supervised learning has typically referred to learning from labeled data, while unsupervised learning has typically referred to learning from unlabeled data. In this paper, we assert that all machine learning is in fact supervised to some degree, and that the scope of supervision is necessarily commensurate to the scope of learning potential. In particular, we argue that clustering algorithms such as k-means, and dimensionality reduction algorithms such as principal component analysis, variational autoencoders, and deep belief networks are each internally supervised by the data itself to learn their respective representations of its features. Furthermore, these algorithms are not capable of external inference until their respective outputs (clusters, principal components, or representation codes) have been identified and externally labeled in effect. As such, they do not suffice as examples of unsupervised learning. We propose that the categorization `supervised vs unsupervised learning' be dispensed with, and instead, learning algorithms be categorized as either $internally~or~externally~supervised$ (or both). We believe this change in perspective will yield new fundamental insights into the structure and character of data and of learning algorithms.

Generative Adversarial Networks Synthesize Realistic OCT Images of the Retina

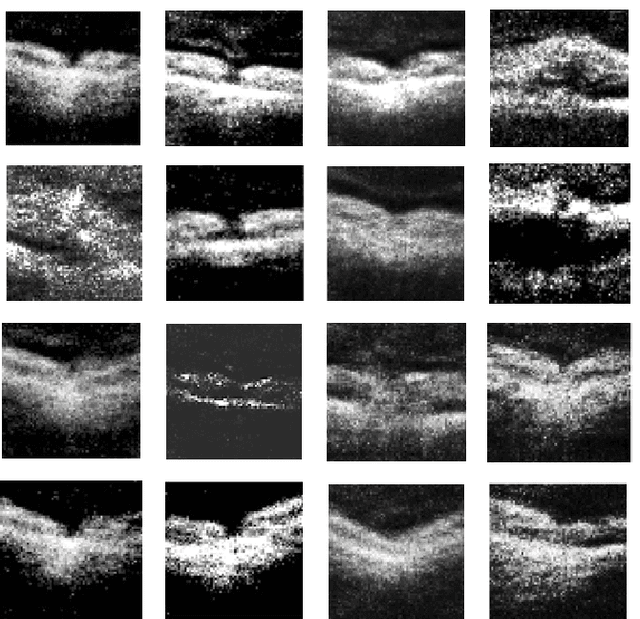
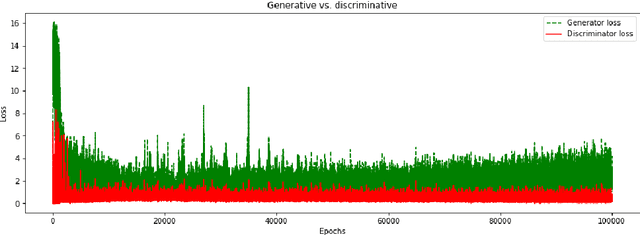
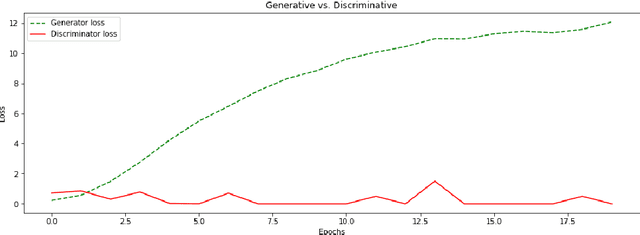
We report, to our knowledge, the first end-to-end application of Generative Adversarial Networks (GANs) towards the synthesis of Optical Coherence Tomography (OCT) images of the retina. Generative models have gained recent attention for the increasingly realistic images they can synthesize, given a sampling of a data type. In this paper, we apply GANs to a sampling distribution of OCTs of the retina. We observe the synthesis of realistic OCT images depicting recognizable pathology such as macular holes, choroidal neovascular membranes, myopic degeneration, cystoid macular edema, and central serous retinopathy amongst others. This represents the first such report of its kind. Potential applications of this new technology include for surgical simulation, for treatment planning, for disease prognostication, and for accelerating the development of new drugs and surgical procedures to treat retinal disease.

Mobile Artificial Intelligence Technology for Detecting Macula Edema and Subretinal Fluid on OCT Scans: Initial Results from the DATUM alpha Study

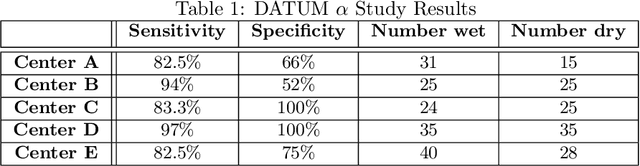
Artificial Intelligence (AI) is necessary to address the large and growing deficit in retina and healthcare access globally. And mobile AI diagnostic platforms running in the Cloud may effectively and efficiently distribute such AI capability. Here we sought to evaluate the feasibility of Cloud-based mobile artificial intelligence for detection of retinal disease. And to evaluate the accuracy of a particular such system for detection of subretinal fluid (SRF) and macula edema (ME) on OCT scans. A multicenter retrospective image analysis was conducted in which board-certified ophthalmologists with fellowship training in retina evaluated OCT images of the macula. They noted the presence or absence of ME or SRF, then compared their assessment to that obtained from Fluid Intelligence, a mobile AI app that detects SRF and ME on OCT scans. Investigators consecutively selected retinal OCTs, while making effort to balance the number of scans with retinal fluid and scans without. Exclusion criteria included poor scan quality, ambiguous features, macula holes, retinoschisis, and dense epiretinal membranes. Accuracy in the form of sensitivity and specificity of the AI mobile App was determined by comparing its assessments to those of the retina specialists. At the time of this submission, five centers have completed their initial studies. This consists of a total of 283 OCT scans of which 155 had either ME or SRF ("wet") and 128 did not ("dry"). The sensitivity ranged from 82.5% to 97% with a weighted average of 89.3%. The specificity ranged from 52% to 100% with a weighted average of 81.23%. CONCLUSION: Cloud-based Mobile AI technology is feasible for the detection retinal disease. In particular, Fluid Intelligence (alpha version), is sufficiently accurate as a screening tool for SRF and ME, especially in underserved areas. Further studies and technology development is needed.

A Sinc Wavelet Describes the Receptive Fields of Neurons in the Motion Cortex

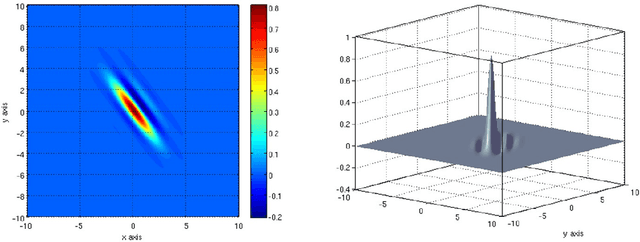
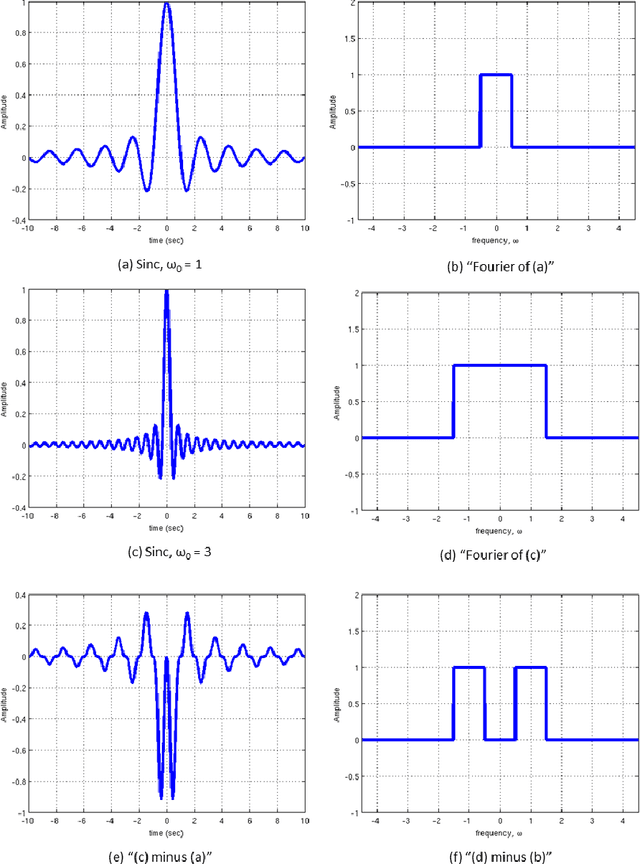
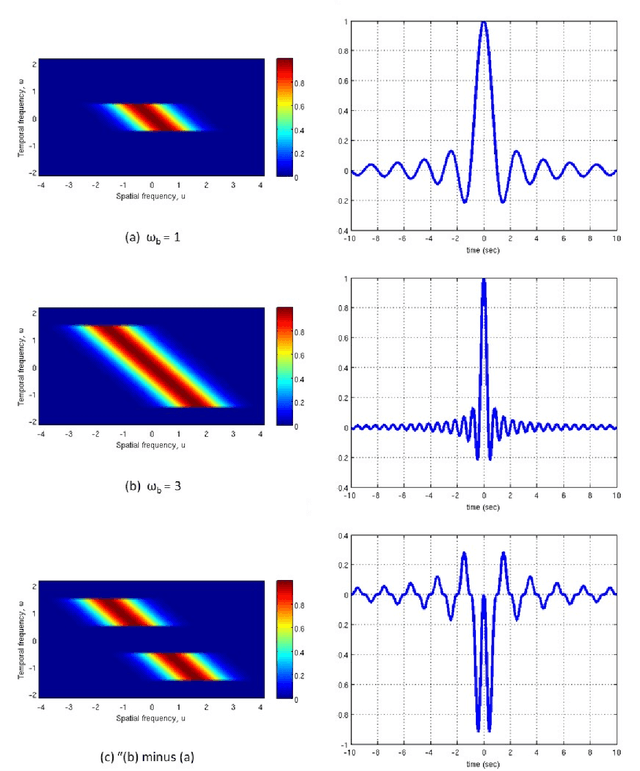
Visual perception results from a systematic transformation of the information flowing through the visual system. In the neuronal hierarchy, the response properties of single neurons are determined by neurons located one level below, and in turn, determine the responses of neurons located one level above. Therefore in modeling receptive fields, it is essential to ensure that the response properties of neurons in a given level can be generated by combining the response models of neurons in its input levels. However, existing response models of neurons in the motion cortex do not inherently yield the temporal frequency filtering gradient (TFFG) property that is known to emerge along the primary visual cortex (V1) to middle temporal (MT) motion processing stream. TFFG is the change from predominantly lowpass to predominantly bandpass temporal frequency filtering character along the V1 to MT pathway (Foster et al 1985; DeAngelis et al 1993; Hawken et al 1996). We devised a new model, the sinc wavelet model (Odaibo, 2014), which logically and efficiently generates the TFFG. The model replaces the Gabor function's sine wave carrier with a sinc (sin(x)/x) function, and has the same or fewer number of parameters as existing models. Because of its logical consistency with the emergent network property of TFFG, we conclude that the sinc wavelet is a better model for the receptive fields of motion cortex neurons. This model will provide new physiological insights into how the brain represents visual information.

The Gabor-Einstein Wavelet: A Model for the Receptive Fields of V1 to MT Neurons

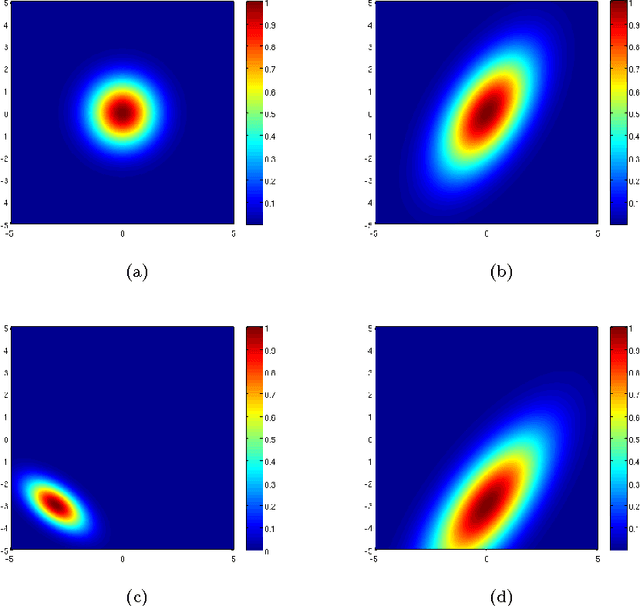
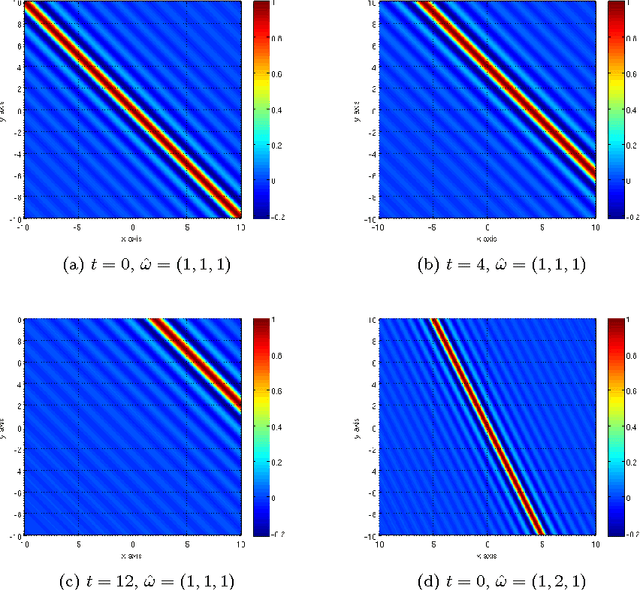
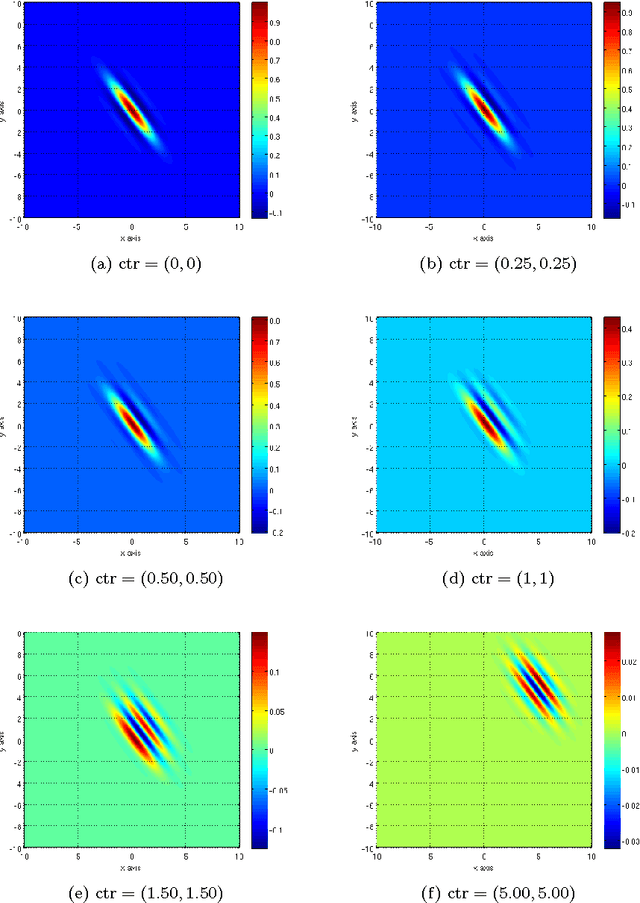
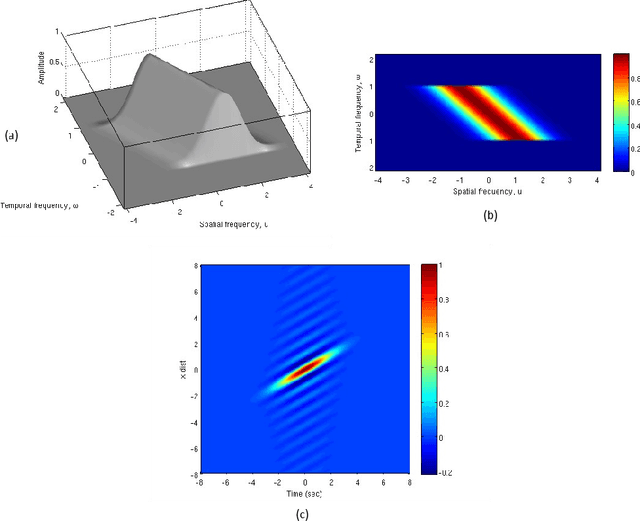
Our visual system is astonishingly efficient at detecting moving objects. This process is mediated by the neurons which connect the primary visual cortex (V1) to the middle temporal (MT) area. Interestingly, since Kuffler's pioneering experiments on retinal ganglion cells, mathematical models have been vital for advancing our understanding of the receptive fields of visual neurons. However, existing models were not designed to describe the most salient attributes of the highly specialized neurons in the V1 to MT motion processing stream; and they have not been able to do so. Here, we introduce the Gabor-Einstein wavelet, a new family of functions for representing the receptive fields of V1 to MT neurons. We show that the way space and time are mixed in the visual cortex is analogous to the way they are mixed in the special theory of relativity (STR). Hence we constrained the Gabor-Einstein model by requiring: (i) relativistic-invariance of the wave carrier, and (ii) the minimum possible number of parameters. From these two constraints, the sinc function emerged as a natural descriptor of the wave carrier. The particular distribution of lowpass to bandpass temporal frequency filtering properties of V1 to MT neurons (Foster et al 1985; DeAngelis et al 1993b; Hawken et al 1996) is clearly explained by the Gabor-Einstein basis. Furthermore, it does so in a manner innately representative of the motion-processing stream's neuronal hierarchy. Our analysis and computer simulations show that the distribution of temporal frequency filtering properties along the motion processing stream is a direct effect of the way the brain jointly encodes space and time. We uncovered this fundamental link by demonstrating that analogous mathematical structures underlie STR and joint cortical spacetime encoding. This link will provide new physiological insights into how the brain represents visual information.