The Gabor-Einstein Wavelet: A Model for the Receptive Fields of V1 to MT Neurons

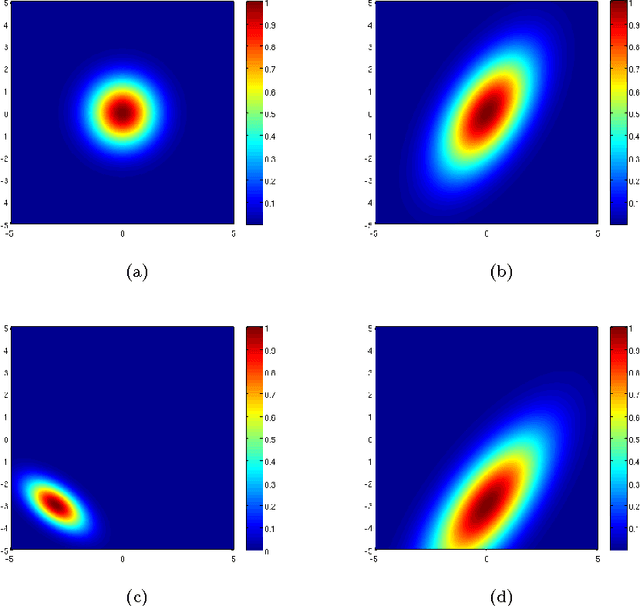
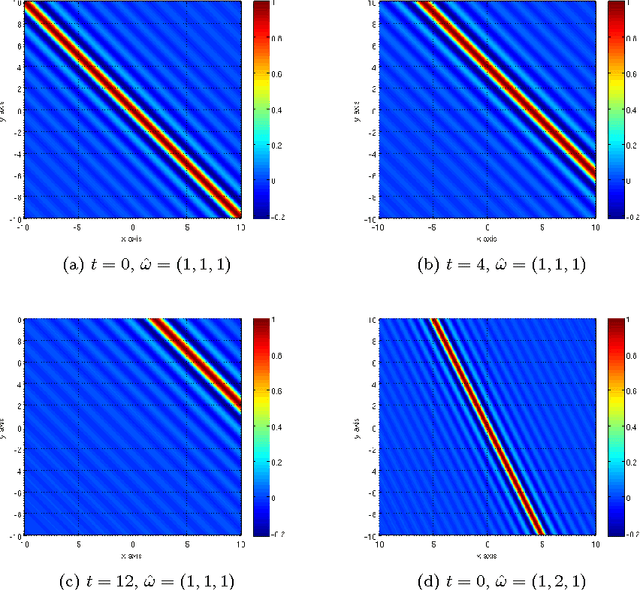
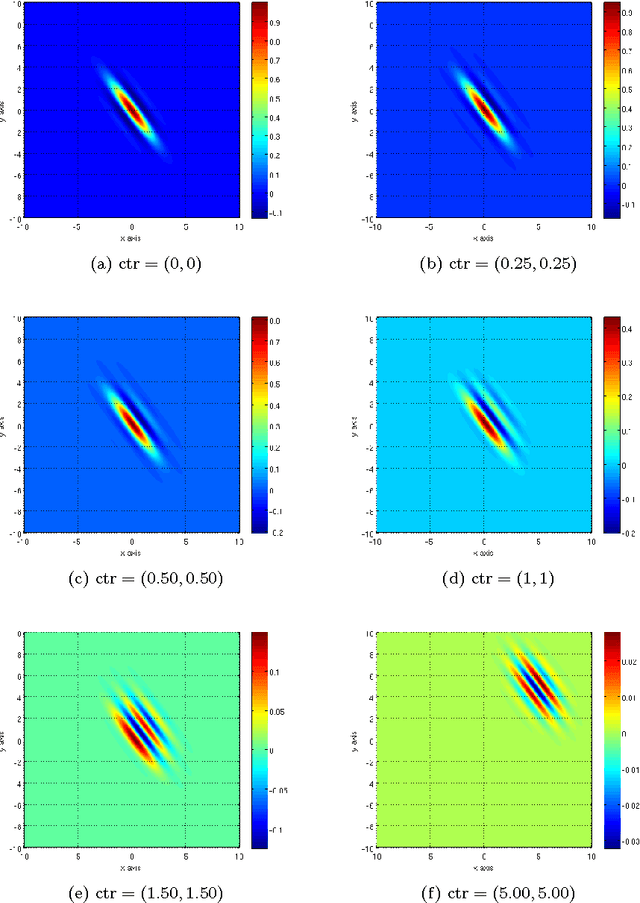
Our visual system is astonishingly efficient at detecting moving objects. This process is mediated by the neurons which connect the primary visual cortex (V1) to the middle temporal (MT) area. Interestingly, since Kuffler's pioneering experiments on retinal ganglion cells, mathematical models have been vital for advancing our understanding of the receptive fields of visual neurons. However, existing models were not designed to describe the most salient attributes of the highly specialized neurons in the V1 to MT motion processing stream; and they have not been able to do so. Here, we introduce the Gabor-Einstein wavelet, a new family of functions for representing the receptive fields of V1 to MT neurons. We show that the way space and time are mixed in the visual cortex is analogous to the way they are mixed in the special theory of relativity (STR). Hence we constrained the Gabor-Einstein model by requiring: (i) relativistic-invariance of the wave carrier, and (ii) the minimum possible number of parameters. From these two constraints, the sinc function emerged as a natural descriptor of the wave carrier. The particular distribution of lowpass to bandpass temporal frequency filtering properties of V1 to MT neurons (Foster et al 1985; DeAngelis et al 1993b; Hawken et al 1996) is clearly explained by the Gabor-Einstein basis. Furthermore, it does so in a manner innately representative of the motion-processing stream's neuronal hierarchy. Our analysis and computer simulations show that the distribution of temporal frequency filtering properties along the motion processing stream is a direct effect of the way the brain jointly encodes space and time. We uncovered this fundamental link by demonstrating that analogous mathematical structures underlie STR and joint cortical spacetime encoding. This link will provide new physiological insights into how the brain represents visual information.