Cluster-Based Autoencoders for Volumetric Point Clouds

Autoencoders allow to reconstruct a given input from a small set of parameters. However, the input size is often limited due to computational costs. We therefore propose a clustering and reassembling method for volumetric point clouds, in order to allow high resolution data as input. We furthermore present an autoencoder based on the well-known FoldingNet for volumetric point clouds and discuss how our approach can be utilized for blending between high resolution point clouds as well as for transferring a volumetric design/style onto a pointcloud while maintaining its shape.

A Joint Deep Learning Approach for Automated Liver and Tumor Segmentation

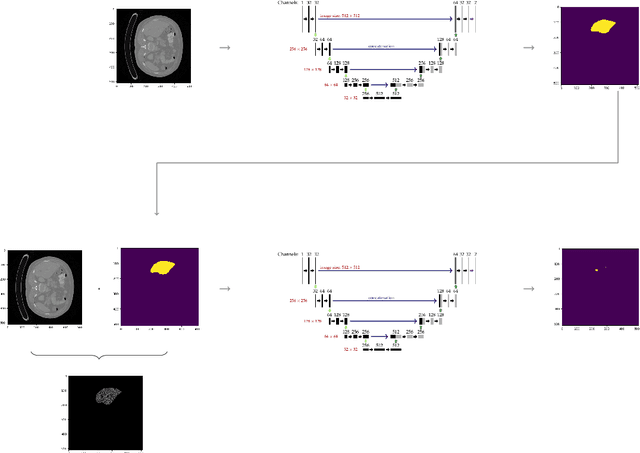
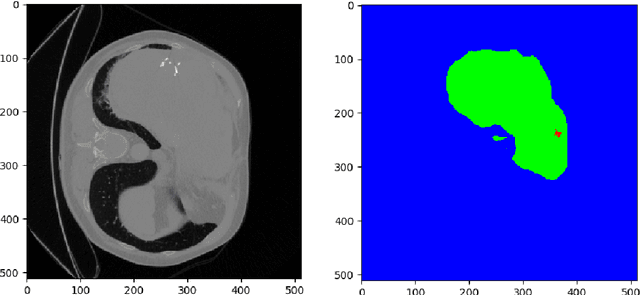
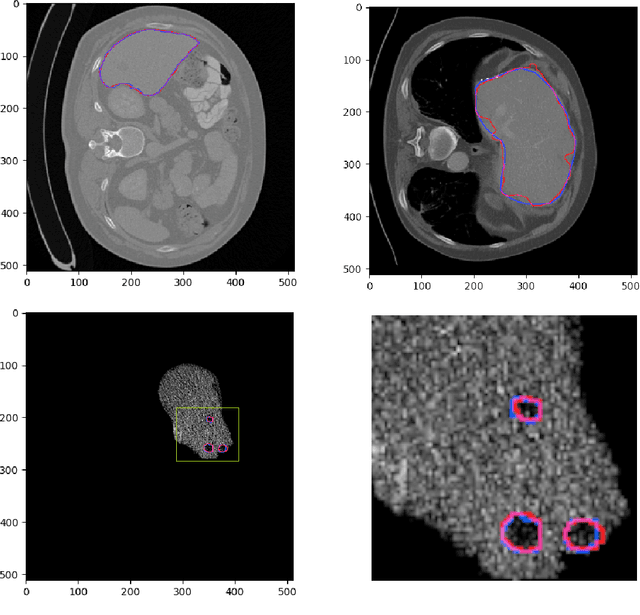
Hepatocellular carcinoma (HCC) is the most common type of primary liver cancer in adults, and the most common cause of death of people suffering from cirrhosis. The segmentation of liver lesions in CT images allows assessment of tumor load, treatment planning, prognosis and monitoring of treatment response. Manual segmentation is a very time-consuming task and in many cases, prone to inaccuracies and automatic tools for tumor detection and segmentation are desirable. In this paper, we use a network architecture that consists of two consecutive fully convolutional neural networks. The first network segments the liver whereas the second network segments the actual tumor inside the liver. Our network is trained on a subset of the LiTS (Liver Tumor Segmentation) challenge and evaluated on data provided from the radiological center in Innsbruck.

NETT: Solving Inverse Problems with Deep Neural Networks

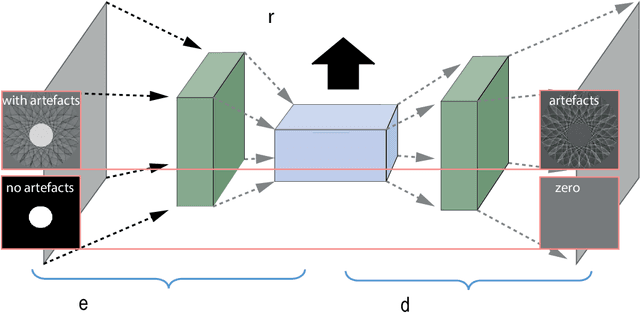
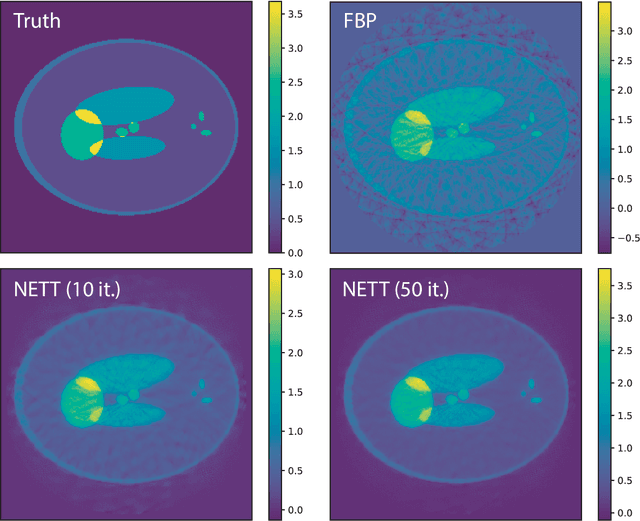
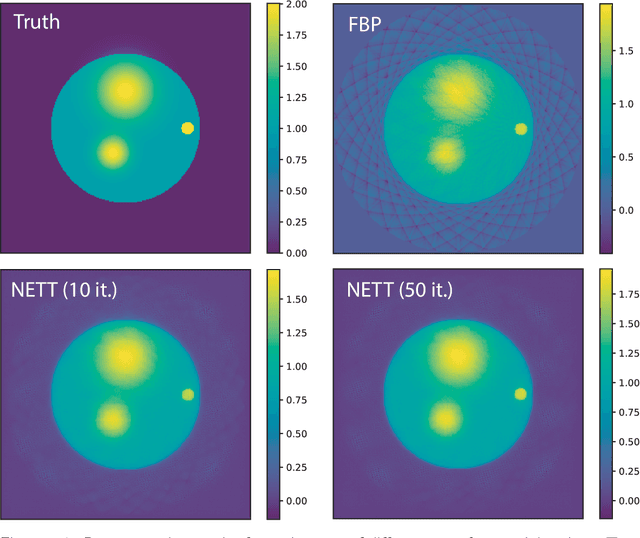
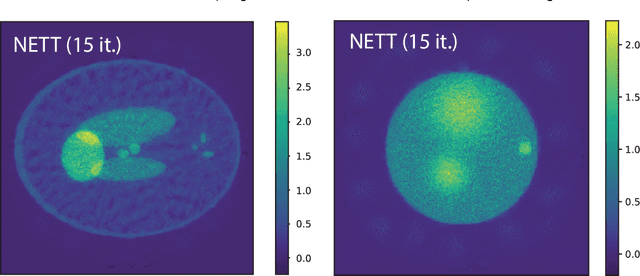
Recovering a function or high-dimensional parameter vector from indirect measurements is a central task in various scientific areas. Several methods for solving such inverse problems are well developed and well understood. Recently, novel algorithms using deep learning and neural networks for inverse problems appeared. While still in their infancy, these techniques show astonishing performance for applications like low-dose CT or various sparse data problems. However, theoretical results for deep learning in inverse problems are missing so far. In this paper, we establish such a convergence analysis for the proposed NETT (Network Tikhonov) approach to inverse problems. NETT considers regularized solutions having small value of a regularizer defined by a trained neural network. Opposed to existing deep learning approaches, our regularization scheme enforces data consistency also for the actual unknown to be recovered. This is beneficial in case the unknown to be recovered is not sufficiently similar to available training data. We present a complete convergence analysis for NETT, where we derive well-posedness results and quantitative error estimates, and propose a possible strategy for training the regularizer. Numerical results are presented for a tomographic sparse data problem using the $\ell^q$-norm of auto-encoder as trained regularizer, which demonstrate good performance of NETT even for unknowns of different type from the training data.