Stefan Keselj
Pushing the Limits of Capsule Networks
Mar 15, 2021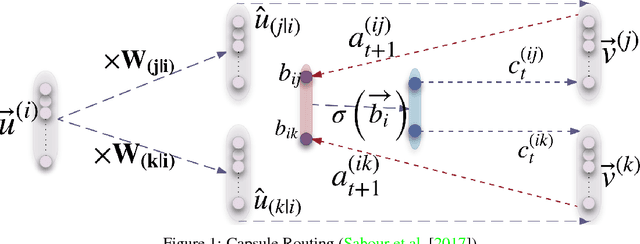

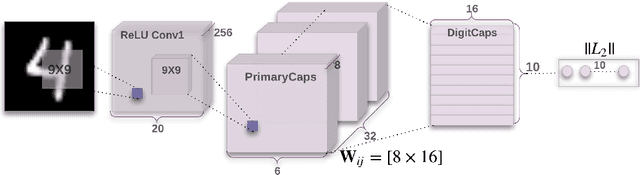

Abstract:Convolutional neural networks use pooling and other downscaling operations to maintain translational invariance for detection of features, but in their architecture they do not explicitly maintain a representation of the locations of the features relative to each other. This means they do not represent two instances of the same object in different orientations the same way, like humans do, and so training them often requires extensive data augmentation and exceedingly deep networks. A team at Google Brain recently made news with an attempt to fix this problem: Capsule Networks. While a normal CNN works with scalar outputs representing feature presence, a CapsNet works with vector outputs representing entity presence. We want to stress test CapsNet in various incremental ways to better understand their performance and expressiveness. In broad terms, the goals of our investigation are: (1) test CapsNets on datasets that are like MNIST but harder in a specific way, and (2) explore the internal embedding space and sources of error for CapsNets.
Siamese Encoding and Alignment by Multiscale Learning with Self-Supervision
Apr 04, 2019
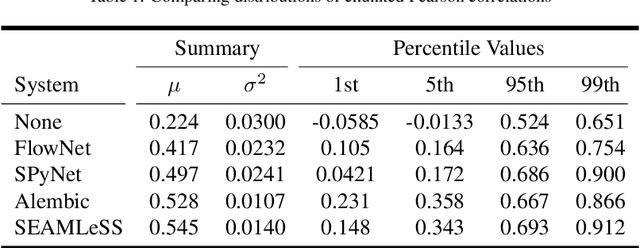
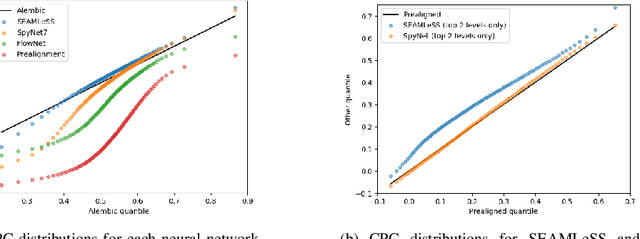

Abstract:We propose a method of aligning a source image to a target image, where the transform is specified by a dense vector field. The two images are encoded as feature hierarchies by siamese convolutional nets. Then a hierarchy of aligner modules computes the transform in a coarse-to-fine recursion. Each module receives as input the transform that was computed by the module at the level above, aligns the source and target encodings at the same level of the hierarchy, and then computes an improved approximation to the transform using a convolutional net. The entire architecture of encoder and aligner nets is trained in a self-supervised manner to minimize the squared error between source and target remaining after alignment. We show that siamese encoding enables more accurate alignment than the image pyramids of SPyNet, a previous deep learning approach to coarse-to-fine alignment. Furthermore, self-supervision applies even without target values for the transform, unlike the strongly supervised SPyNet. We also show that our approach outperforms one-shot approaches to alignment, because the fine pathways in the latter approach may fail to contribute to alignment accuracy when displacements are large. As shown by previous one-shot approaches, good results from self-supervised learning require that the loss function additionally penalize non-smooth transforms. We demonstrate that "masking out" the penalty function near discontinuities leads to correct recovery of non-smooth transforms. Our claims are supported by empirical comparisons using images from serial section electron microscopy of brain tissue.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge