Multi-Robot Informative Path Planning from Regression with Sparse Gaussian Processes

This paper addresses multi-robot informative path planning (IPP) for environmental monitoring. The problem involves determining informative regions in the environment that should be visited by robots in order to gather the most amount of information about the environment. We propose an efficient sparse Gaussian process-based approach that uses gradient descent to optimize paths in continuous environments. Our approach efficiently scales to both spatially and spatio-temporally correlated environments. Moreover, our approach can simultaneously optimize the informative paths while accounting for routing constraints, such as a distance budget and limits on the robot's velocity and acceleration. Our approach can be used for IPP with both discrete and continuous sensing robots, with point and non-point field-of-view sensing shapes, and for both single and multi-robot IPP. We demonstrate that the proposed approach is fast and accurate on real-world data.

Efficient Sensor Placement from Regression with Sparse Gaussian Processes in Continuous and Discrete Spaces

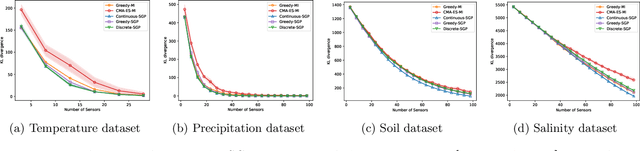
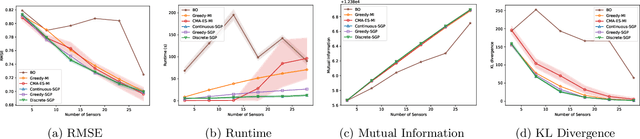
We present a novel approach based on sparse Gaussian processes (SGPs) to address the sensor placement problem for monitoring spatially (or spatiotemporally) correlated phenomena such as temperature. Existing Gaussian process (GP) based sensor placement approaches use GPs to model the phenomena and subsequently optimize the sensor locations in a discretized representation of the environment. In our approach, we fit an SGP to randomly sampled unlabeled locations in the environment and show that the learned inducing points of the SGP inherently solve the sensor placement problem in continuous spaces. Using SGPs avoids discretizing the environment and reduces the computation cost from cubic to linear complexity. When restricted to a candidate set of sensor placement locations, we can use greedy sequential selection algorithms on the SGP's optimization bound to find good solutions. We also present an approach to efficiently map our continuous space solutions to discrete solution spaces using the assignment problem, which gives us discrete sensor placements optimized in unison. Moreover, we generalize our approach to model non-point sensors with an arbitrary field-of-view (FoV) shape using an efficient transformation technique. Finally, we leverage theoretical results from the SGP literature to bound the number of required sensors and the quality of the solution placements. Our experimental results on two real-world datasets show that our approaches generate solutions consistently on par with the prior state-of-the-art approach while being substantially faster. We also demonstrate our solution placements for non-point FoV sensors and a spatiotemporally correlated phenomenon on a scale that was previously infeasible.

Area Coverage with Multiple Capacity-Constrained Robots

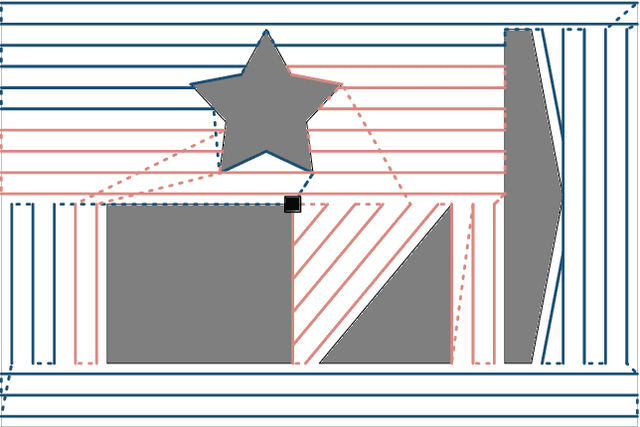
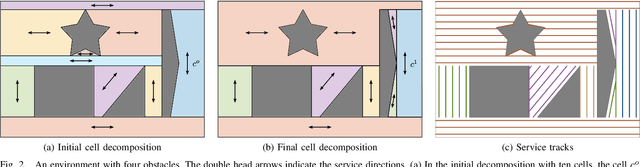
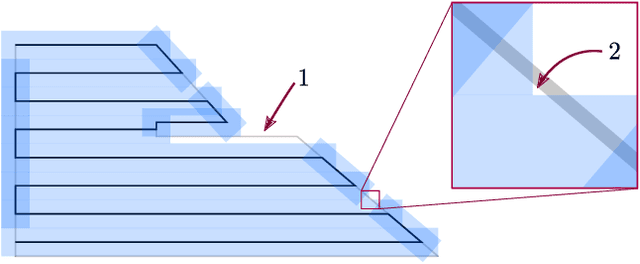
The area coverage problem is the task of efficiently servicing a given two-dimensional surface using sensors mounted on robots such as unmanned aerial vehicles (UAVs) and unmanned ground vehicles (UGVs). We present a novel formulation for generating coverage routes for multiple capacity-constrained robots, where capacity can be specified in terms of battery life or flight time. Traversing the environment incurs demands on the robot resources, which have capacity limits. The central aspect of our approach is transforming the area coverage problem into a line coverage problem (i.e., coverage of linear features), and then generating routes that minimize the total cost of travel while respecting the capacity constraints. We define two modes of travel: (1) servicing and (2) deadheading, which correspond to whether a robot is performing task-specific actions or not. Our formulation allows separate and asymmetric travel costs and demands for the two modes. Furthermore, the cells computed from cell decomposition, aimed at minimizing the number of turns, are not required to be monotone polygons. We develop new procedures for cell decomposition and generation of service tracks that can handle non-monotone polygons with or without holes. We establish the efficacy of our algorithm on a ground robot dataset with 25 indoor environments and an aerial robot dataset with 300 outdoor environments. The algorithm generates solutions whose costs are 10% lower on average than state-of-the-art methods. We additionally demonstrate our algorithm in experiments with UAVs.

The Single Robot Line Coverage Problem: Theory, Algorithms and Experiments

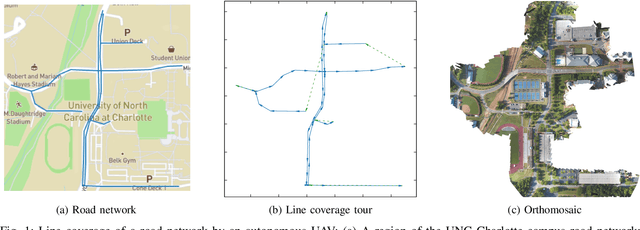
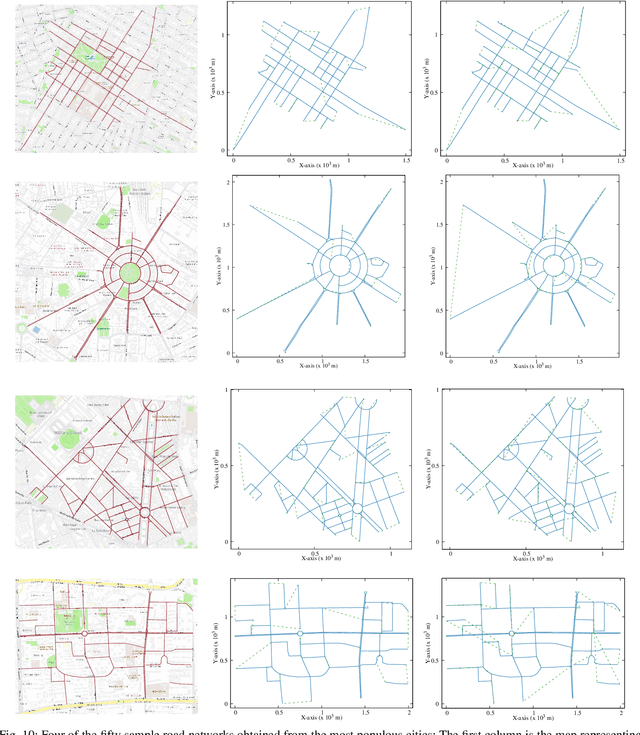
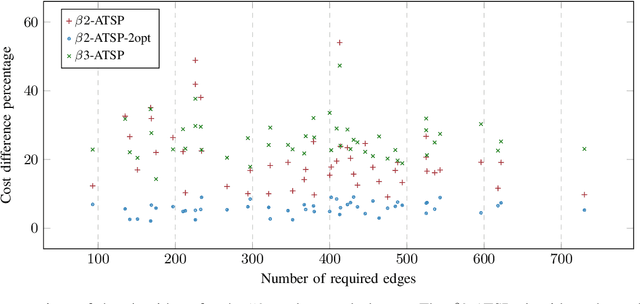
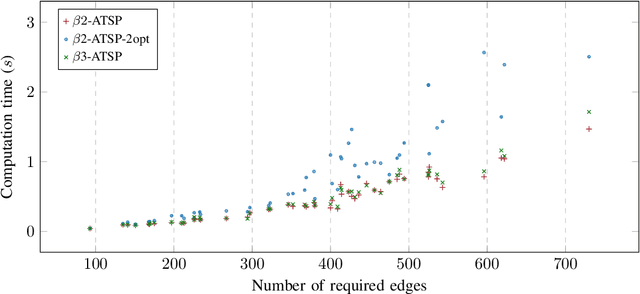
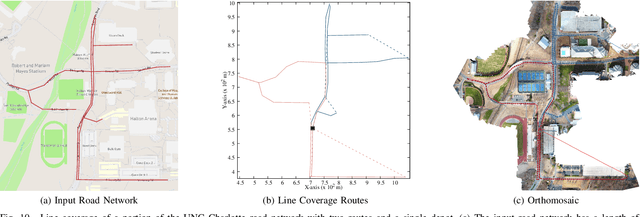
Line coverage is the task of servicing a given set of one-dimensional features in an environment. It is important for the inspection of linear infrastructure such as road networks, power lines, and oil and gas pipelines. This paper addresses the single robot line coverage problem for aerial and ground robots by modeling it as an optimization problem on a graph. The problem belongs to the broad class of arc routing problems and is closely related to the asymmetric rural postman problem (RPP). The paper presents an integer linear programming formulation with proof of correctness. Using the minimum cost flow problem, we develop approximation algorithms with guarantees on the solution quality. These guarantees also improve the existing results for the asymmetric RPP. The main algorithm partitions the problem into three cases based on the structure of the required graph, i.e., the graph induced by the features that require servicing. We evaluate our algorithms on road networks from the 50 most populous cities in the world. The algorithms, augmented with improvement heuristics, run within 3s and generate solutions that are within 10% of the optimum. We experimentally demonstrate our algorithms with commercial UAVs on the UNC Charlotte campus road network.

Line Coverage with Multiple Robots: Algorithms and Experiments

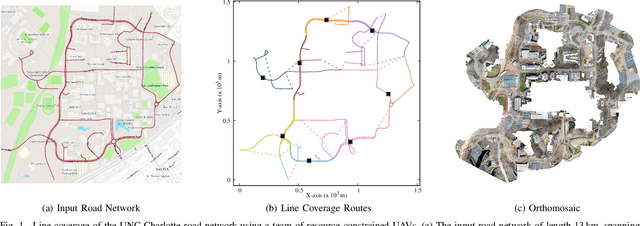
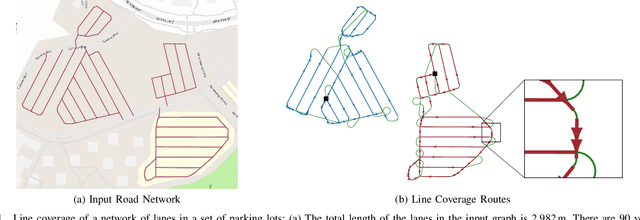
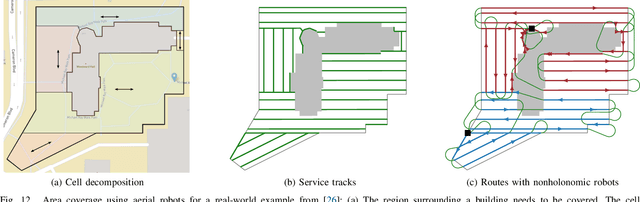
The line coverage problem is to find efficient routes for coverage of linear features by one or more resource-constrained robots. Linear features model environments such as road networks, power lines, and oil and gas pipelines. We define two modes of travel for the robots: servicing and deadheading. A robot services a feature if it performs task-specific actions, e.g., taking images, as it traverses the feature; otherwise, it is deadheading. Traversing the environment incurs costs (e.g., travel time) and demands on resources (e.g., battery life). Servicing and deadheading can have different cost and demand functions, and we further permit them to be direction-dependent. We model the environment as a graph and provide an integer linear program. As the problem is NP-hard, we develop a fast and efficient heuristic algorithm, Merge-Embed-Merge (MEM). The constructive property of the algorithm enables solving the multi-depot version for large graphs. We further extend the MEM algorithm to handle turning costs and nonholonomic constraints. We benchmark the algorithm on a dataset of 50 road networks and demonstrate the algorithm in experiments using aerial robots on road networks.

The Correlated Arc Orienteering Problem

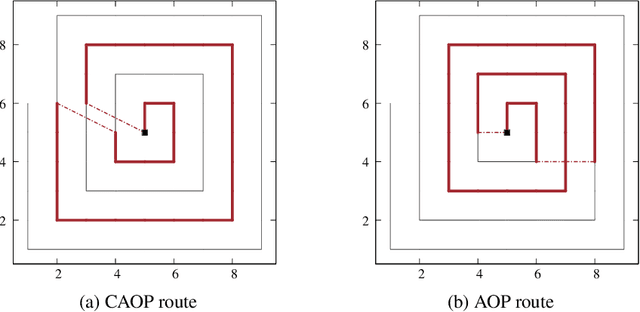
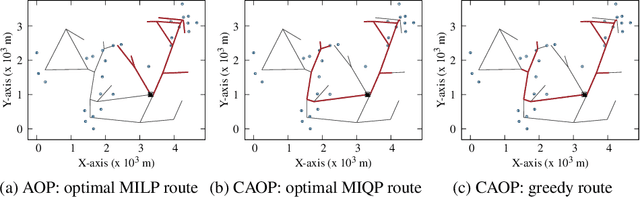
This paper introduces the correlated arc orienteering problem (CAOP), where the task is to find routes for a team of robots to maximize the collection of rewards associated with features in the environment. These features can be one-dimensional or points in the environment, and can have spatial correlation, i.e., visiting a feature in the environment may provide a portion of the reward associated with a correlated feature. A robot incurs costs as it traverses the environment, and the total cost for its route is limited by a resource constraint such as battery life or operation time. As environments are often large, we permit multiple depots where the robots must start and end their routes. The CAOP generalizes the correlated orienteering problem (COP), where the rewards are only associated with point features, and the arc orienteering problem (AOP), where the rewards are not spatially correlated. We formulate a mixed integer quadratic program (MIQP) that formalizes the problem and gives optimal solutions. However, the problem is NP-hard, and therefore we develop an efficient greedy constructive algorithm. We illustrate the problem with two different applications: informative path planning for methane gas leak detection and coverage of road networks.