Efficient Sensor Placement from Regression with Sparse Gaussian Processes in Continuous and Discrete Spaces

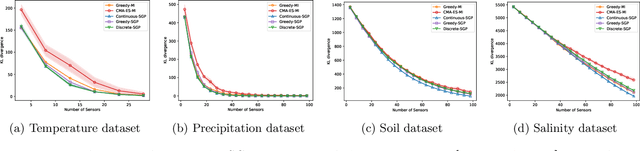
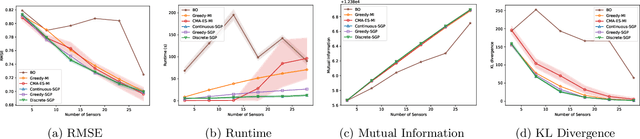
We present a novel approach based on sparse Gaussian processes (SGPs) to address the sensor placement problem for monitoring spatially (or spatiotemporally) correlated phenomena such as temperature. Existing Gaussian process (GP) based sensor placement approaches use GPs to model the phenomena and subsequently optimize the sensor locations in a discretized representation of the environment. In our approach, we fit an SGP to randomly sampled unlabeled locations in the environment and show that the learned inducing points of the SGP inherently solve the sensor placement problem in continuous spaces. Using SGPs avoids discretizing the environment and reduces the computation cost from cubic to linear complexity. When restricted to a candidate set of sensor placement locations, we can use greedy sequential selection algorithms on the SGP's optimization bound to find good solutions. We also present an approach to efficiently map our continuous space solutions to discrete solution spaces using the assignment problem, which gives us discrete sensor placements optimized in unison. Moreover, we generalize our approach to model non-point sensors with an arbitrary field-of-view (FoV) shape using an efficient transformation technique. Finally, we leverage theoretical results from the SGP literature to bound the number of required sensors and the quality of the solution placements. Our experimental results on two real-world datasets show that our approaches generate solutions consistently on par with the prior state-of-the-art approach while being substantially faster. We also demonstrate our solution placements for non-point FoV sensors and a spatiotemporally correlated phenomenon on a scale that was previously infeasible.