Line Coverage with Multiple Robots: Algorithms and Experiments
Paper and Code
Aug 19, 2022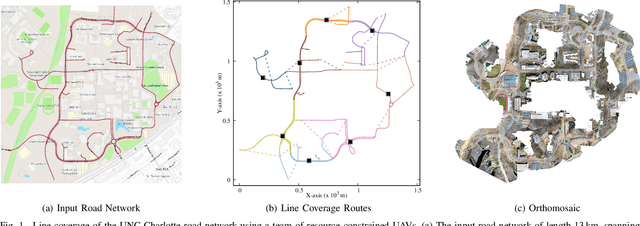
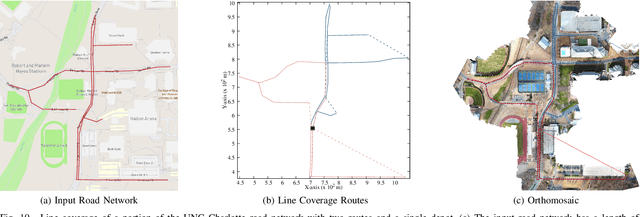
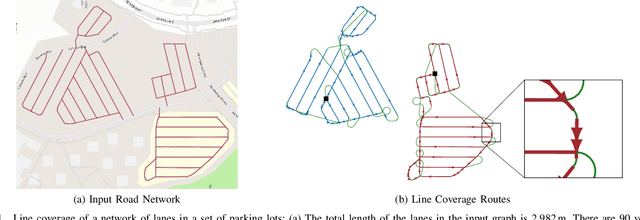
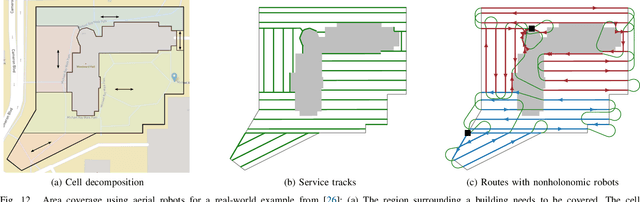
The line coverage problem is to find efficient routes for coverage of linear features by one or more resource-constrained robots. Linear features model environments such as road networks, power lines, and oil and gas pipelines. We define two modes of travel for the robots: servicing and deadheading. A robot services a feature if it performs task-specific actions, e.g., taking images, as it traverses the feature; otherwise, it is deadheading. Traversing the environment incurs costs (e.g., travel time) and demands on resources (e.g., battery life). Servicing and deadheading can have different cost and demand functions, and we further permit them to be direction-dependent. We model the environment as a graph and provide an integer linear program. As the problem is NP-hard, we develop a fast and efficient heuristic algorithm, Merge-Embed-Merge (MEM). The constructive property of the algorithm enables solving the multi-depot version for large graphs. We further extend the MEM algorithm to handle turning costs and nonholonomic constraints. We benchmark the algorithm on a dataset of 50 road networks and demonstrate the algorithm in experiments using aerial robots on road networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge