Soren Forchhammer
Incorporating Prior Information in Compressive Online Robust Principal Component Analysis
May 27, 2017
Abstract:We consider an online version of the robust Principle Component Analysis (PCA), which arises naturally in time-varying source separations such as video foreground-background separation. This paper proposes a compressive online robust PCA with prior information for recursively separating a sequences of frames into sparse and low-rank components from a small set of measurements. In contrast to conventional batch-based PCA, which processes all the frames directly, the proposed method processes measurements taken from each frame. Moreover, this method can efficiently incorporate multiple prior information, namely previous reconstructed frames, to improve the separation and thereafter, update the prior information for the next frame. We utilize multiple prior information by solving $n\text{-}\ell_{1}$ minimization for incorporating the previous sparse components and using incremental singular value decomposition ($\mathrm{SVD}$) for exploiting the previous low-rank components. We also establish theoretical bounds on the number of measurements required to guarantee successful separation under assumptions of static or slowly-changing low-rank components. Using numerical experiments, we evaluate our bounds and the performance of the proposed algorithm. In addition, we apply the proposed algorithm to online video foreground and background separation from compressive measurements. Experimental results show that the proposed method outperforms the existing methods.
Measurement Bounds for Sparse Signal Reconstruction with Multiple Side Information
Jan 18, 2017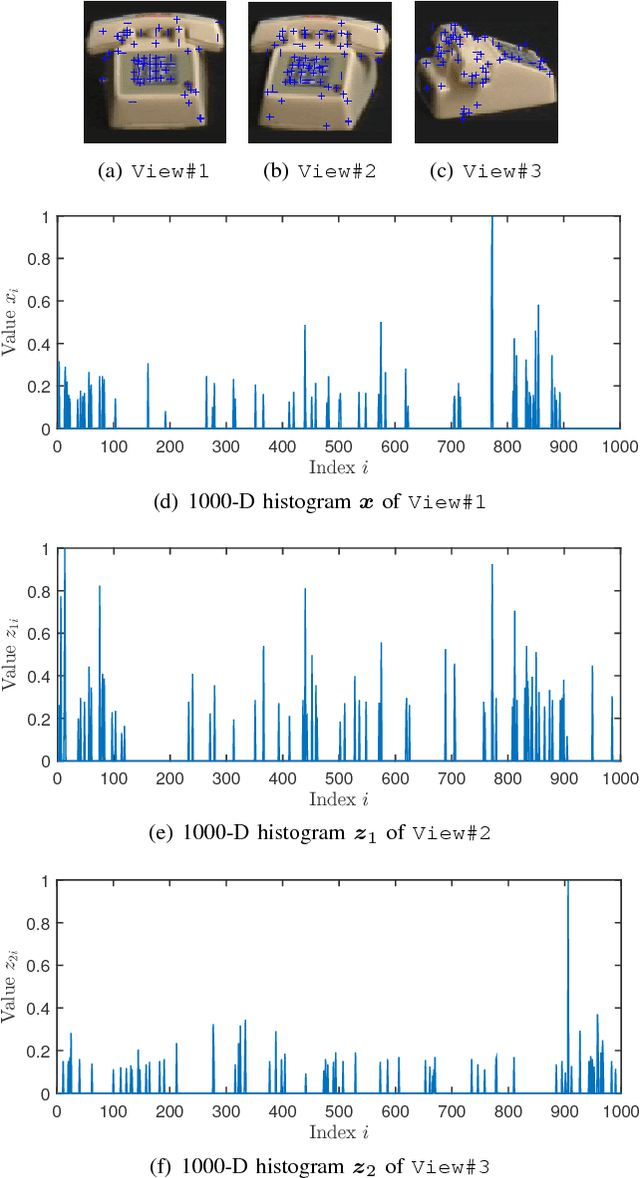
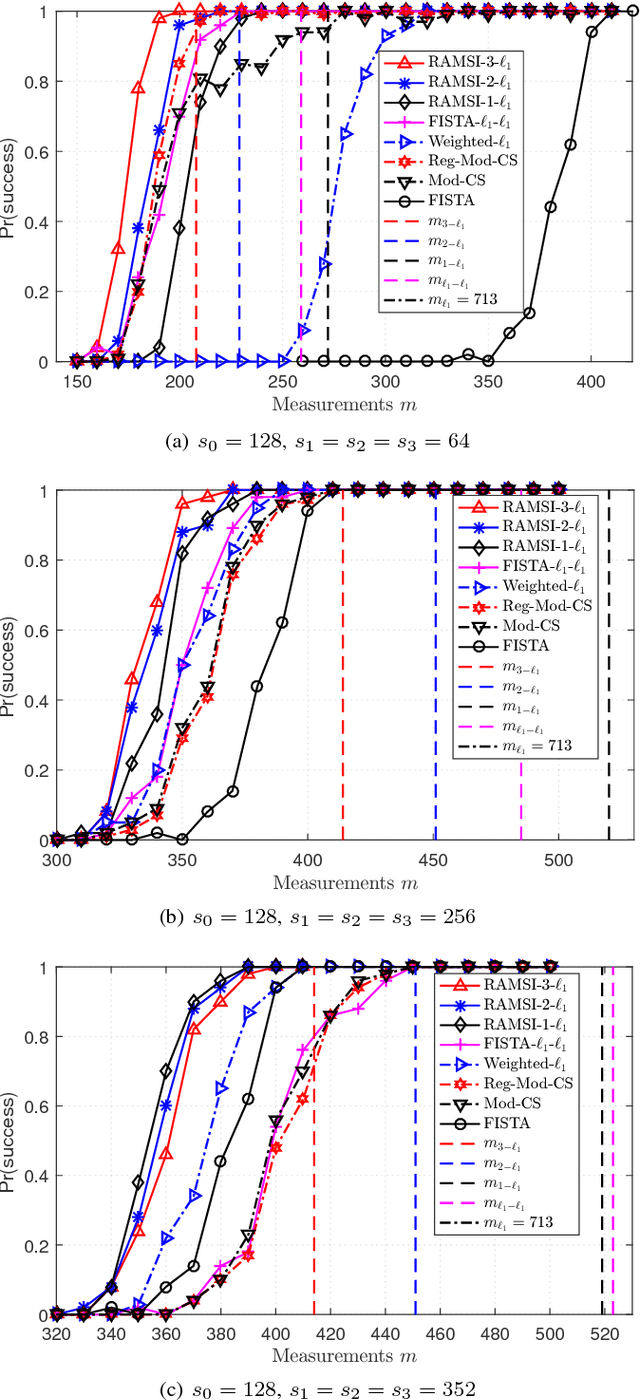
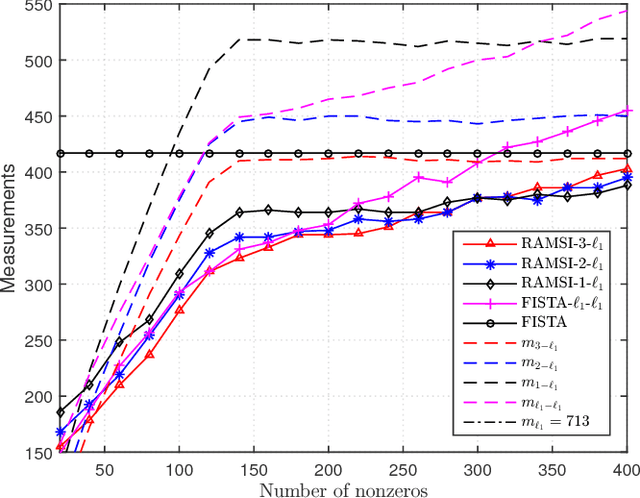
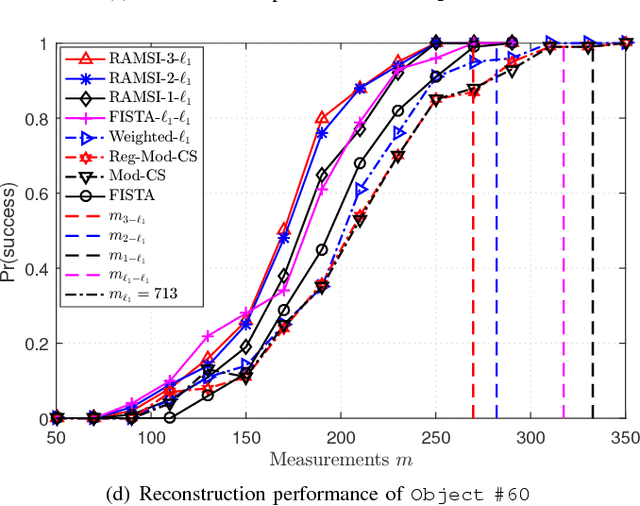
Abstract:In the context of compressed sensing (CS), this paper considers the problem of reconstructing sparse signals with the aid of other given correlated sources as multiple side information. To address this problem, we theoretically study a generic \textcolor{black}{weighted $n$-$\ell_{1}$ minimization} framework and propose a reconstruction algorithm that leverages multiple side information signals (RAMSI). The proposed RAMSI algorithm computes adaptively optimal weights among the side information signals at every reconstruction iteration. In addition, we establish theoretical bounds on the number of measurements that are required to successfully reconstruct the sparse source by using \textcolor{black}{weighted $n$-$\ell_{1}$ minimization}. The analysis of the established bounds reveal that \textcolor{black}{weighted $n$-$\ell_{1}$ minimization} can achieve sharper bounds and significant performance improvements compared to classical CS. We evaluate experimentally the proposed RAMSI algorithm and the established bounds using synthetic sparse signals as well as correlated feature histograms, extracted from a multiview image database for object recognition. The obtained results show clearly that the proposed algorithm outperforms state-of-the-art algorithms---\textcolor{black}{including classical CS, $\ell_1\text{-}\ell_1$ minimization, Modified-CS, regularized Modified-CS, and weighted $\ell_1$ minimization}---in terms of both the theoretical bounds and the practical performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge