Measurement Bounds for Sparse Signal Reconstruction with Multiple Side Information
Paper and Code
Jan 18, 2017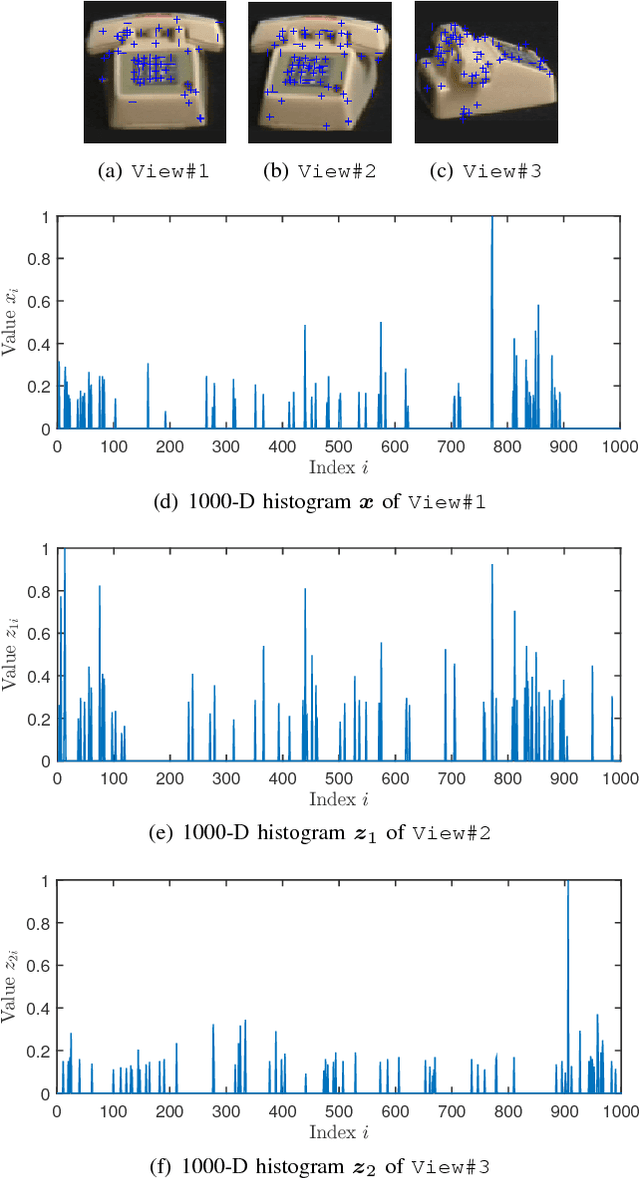
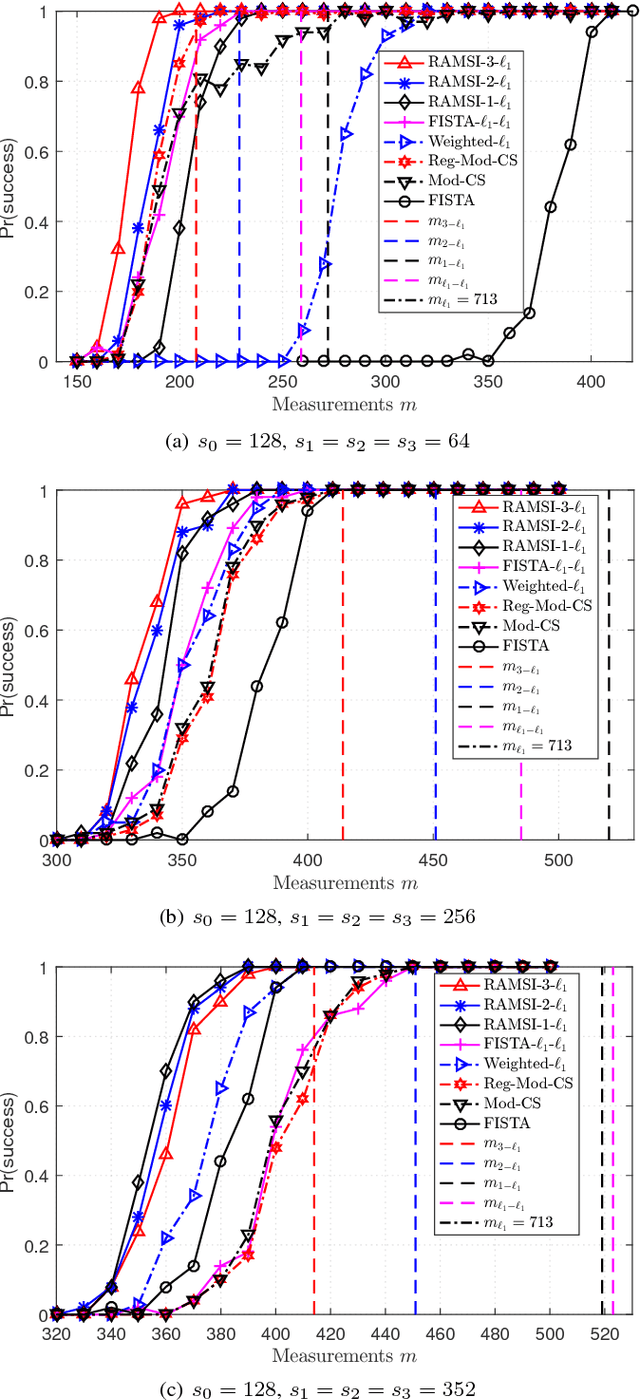
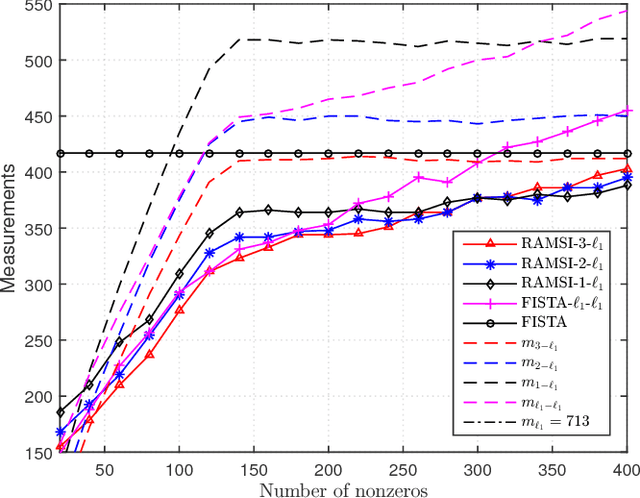
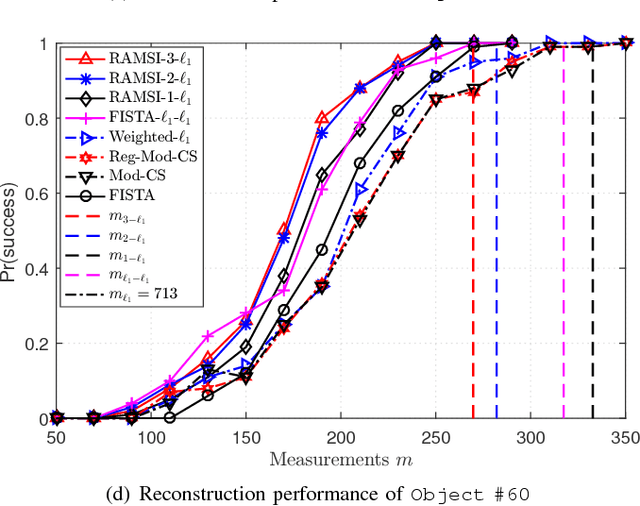
In the context of compressed sensing (CS), this paper considers the problem of reconstructing sparse signals with the aid of other given correlated sources as multiple side information. To address this problem, we theoretically study a generic \textcolor{black}{weighted $n$-$\ell_{1}$ minimization} framework and propose a reconstruction algorithm that leverages multiple side information signals (RAMSI). The proposed RAMSI algorithm computes adaptively optimal weights among the side information signals at every reconstruction iteration. In addition, we establish theoretical bounds on the number of measurements that are required to successfully reconstruct the sparse source by using \textcolor{black}{weighted $n$-$\ell_{1}$ minimization}. The analysis of the established bounds reveal that \textcolor{black}{weighted $n$-$\ell_{1}$ minimization} can achieve sharper bounds and significant performance improvements compared to classical CS. We evaluate experimentally the proposed RAMSI algorithm and the established bounds using synthetic sparse signals as well as correlated feature histograms, extracted from a multiview image database for object recognition. The obtained results show clearly that the proposed algorithm outperforms state-of-the-art algorithms---\textcolor{black}{including classical CS, $\ell_1\text{-}\ell_1$ minimization, Modified-CS, regularized Modified-CS, and weighted $\ell_1$ minimization}---in terms of both the theoretical bounds and the practical performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge