Separability and Scatteredness (S&S) Ratio-Based Efficient SVM Regularization Parameter, Kernel, and Kernel Parameter Selection

Support Vector Machine (SVM) is a robust machine learning algorithm with broad applications in classification, regression, and outlier detection. SVM requires tuning the regularization parameter (RP) which controls the model capacity and the generalization performance. Conventionally, the optimum RP is found by comparison of a range of values through the Cross-Validation (CV) procedure. In addition, for non-linearly separable data, the SVM uses kernels where a set of kernels, each with a set of parameters, denoted as a grid of kernels, are considered. The optimal choice of RP and the grid of kernels is through the grid-search of CV. By stochastically analyzing the behavior of the regularization parameter, this work shows that the SVM performance can be modeled as a function of separability and scatteredness (S&S) of the data. Separability is a measure of the distance between classes, and scatteredness is the ratio of the spread of data points. In particular, for the hinge loss cost function, an S&S ratio-based table provides the optimum RP. The S&S ratio is a powerful value that can automatically detect linear or non-linear separability before using the SVM algorithm. The provided S&S ratio-based table can also provide the optimum kernel and its parameters before using the SVM algorithm. Consequently, the computational complexity of the CV grid-search is reduced to only one time use of the SVM. The simulation results on the real dataset confirm the superiority and efficiency of the proposed approach in the sense of computational complexity over the grid-search CV method.

Learnability, Sample Complexity, and Hypothesis Class Complexity for Regression Models

The goal of a learning algorithm is to receive a training data set as input and provide a hypothesis that can generalize to all possible data points from a domain set. The hypothesis is chosen from hypothesis classes with potentially different complexities. Linear regression modeling is an important category of learning algorithms. The practical uncertainty of the target samples affects the generalization performance of the learned model. Failing to choose a proper model or hypothesis class can lead to serious issues such as underfitting or overfitting. These issues have been addressed by alternating cost functions or by utilizing cross-validation methods. These approaches can introduce new hyperparameters with their own new challenges and uncertainties or increase the computational complexity of the learning algorithm. On the other hand, the theory of probably approximately correct (PAC) aims at defining learnability based on probabilistic settings. Despite its theoretical value, PAC does not address practical learning issues on many occasions. This work is inspired by the foundation of PAC and is motivated by the existing regression learning issues. The proposed approach, denoted by epsilon-Confidence Approximately Correct (epsilon CoAC), utilizes Kullback Leibler divergence (relative entropy) and proposes a new related typical set in the set of hyperparameters to tackle the learnability issue. Moreover, it enables the learner to compare hypothesis classes of different complexity orders and choose among them the optimum with the minimum epsilon in the epsilon CoAC framework. Not only the epsilon CoAC learnability overcomes the issues of overfitting and underfitting, but it also shows advantages and superiority over the well known cross-validation method in the sense of time consumption as well as in the sense of accuracy.

Relative Entropy (RE) Based LTI System Modeling Equipped with time delay Estimation and Online Modeling

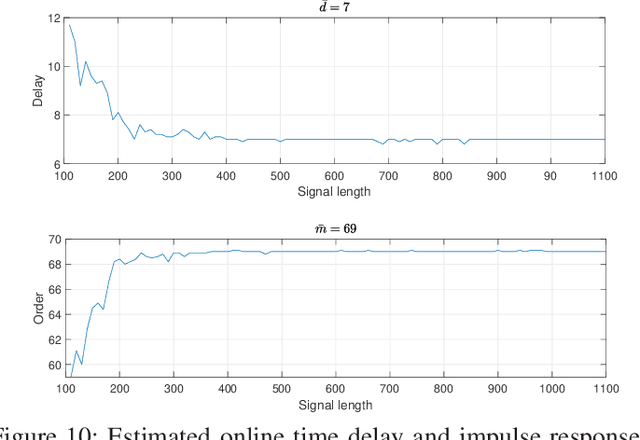
This paper proposes an impulse response modeling in presence of input and noisy output of a linear time-invariant (LTI) system. The approach utilizes Relative Entropy (RE) to choose the optimum impulse response estimate, optimum time delay and optimum impulse response length. The desired RE is the Kulback-Lielber divergence of the estimated distribution from its unknown true distribution. A unique probabilistic validation approach estimates the desired relative entropy and minimizes this criterion to provide the impulse response estimate. Classical methods have approached this system modeling problem from two separate angles for the time delay estimation and for the order selection. Time delay methods focus on time delay estimate minimizing various proposed criteria, while the existing order selection approaches choose the optimum impulse response length based on their proposed criteria. The strength of the proposed RE based method is in using the RE based criterion to estimate both the time delay and impulse response length simultaneously. In addition, estimation of the noise variance, when the Signal to Noise Ratio (SNR) is unknown is also concurrent and is based on optimizing the same RE based criterion. The RE based approach is also extended for online impulse response estimations. The online method reduces the model estimation computational complexity upon the arrival of a new sample. The introduced efficient stopping criteria for this online approaches is extremely valuable in practical applications. Simulation results illustrate precision and efficiency of the proposed method compared to the conventional time delay or order selection approaches.

Hyperspectral Image Classification Based on Sparse Modeling of Spectral Blocks

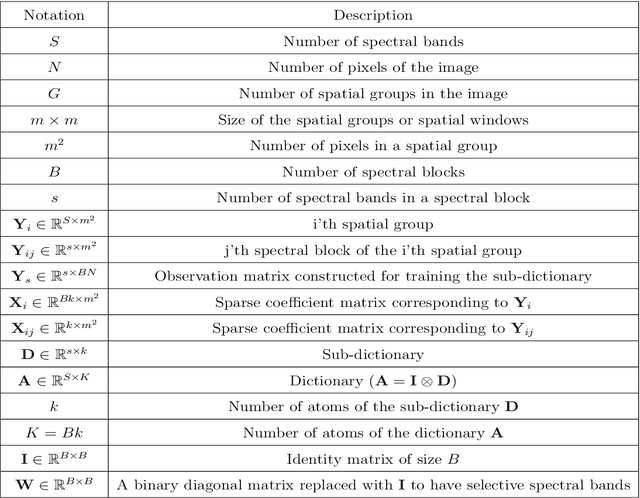
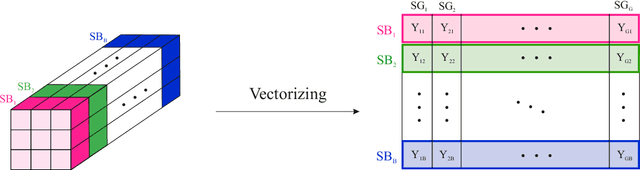
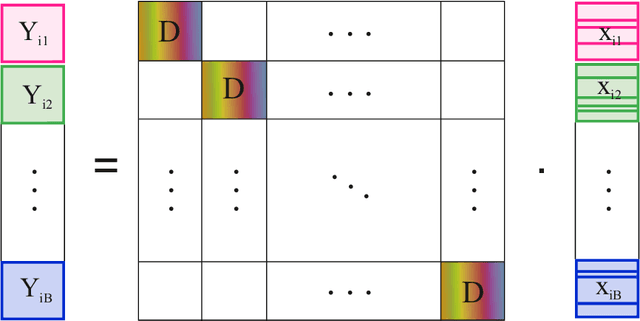
Hyperspectral images provide abundant spatial and spectral information that is very valuable for material detection in diverse areas of practical science. The high-dimensions of data lead to many processing challenges that can be addressed via existent spatial and spectral redundancies. In this paper, a sparse modeling framework is proposed for hyperspectral image classification. Spectral blocks are introduced to be used along with spatial groups to jointly exploit spectral and spatial redundancies. To reduce the computational complexity of sparse modeling, spectral blocks are used to break the high-dimensional optimization problems into small-size sub-problems that are faster to solve. Furthermore, the proposed sparse structure enables to extract the most discriminative spectral blocks and further reduce the computational burden. Experiments on three benchmark datasets, i.e., Pavia University Image and Indian Pines Image verify that the proposed method leads to a robust sparse modeling of hyperspectral images and improves the classification accuracy compared to several state-of-the-art methods. Moreover, the experiments demonstrate that the proposed method requires less processing time.

Efficient Low Dose X-ray CT Reconstruction through Sparsity-Based MAP Modeling

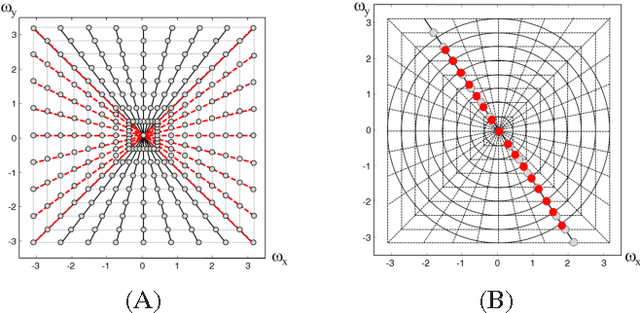
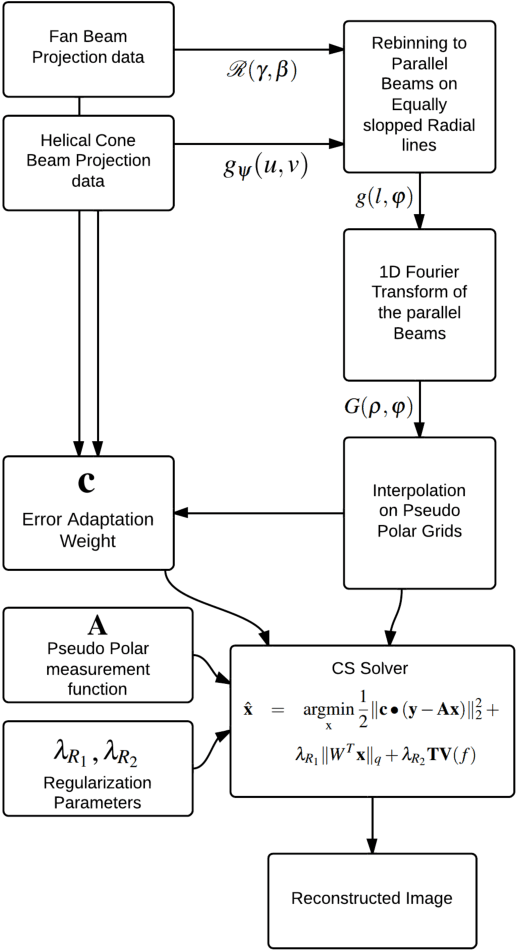
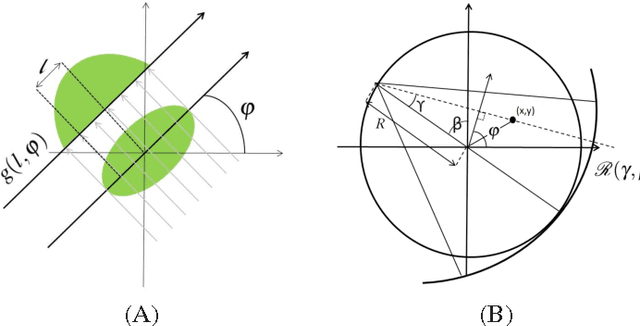
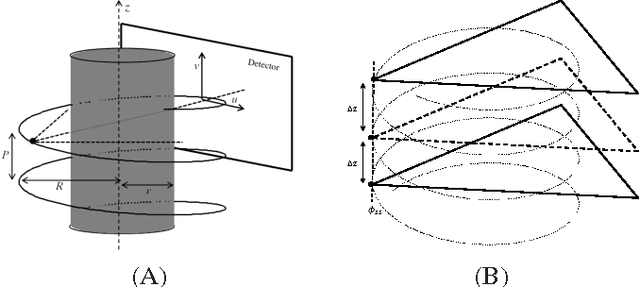
Ultra low radiation dose in X-ray Computed Tomography (CT) is an important clinical objective in order to minimize the risk of carcinogenesis. Compressed Sensing (CS) enables significant reductions in radiation dose to be achieved by producing diagnostic images from a limited number of CT projections. However, the excessive computation time that conventional CS-based CT reconstruction typically requires has limited clinical implementation. In this paper, we first demonstrate that a thorough analysis of CT reconstruction through a Maximum a Posteriori objective function results in a weighted compressive sensing problem. This analysis enables us to formulate a low dose fan beam and helical cone beam CT reconstruction. Subsequently, we provide an efficient solution to the formulated CS problem based on a Fast Composite Splitting Algorithm-Latent Expected Maximization (FCSA-LEM) algorithm. In the proposed method we use pseudo polar Fourier transform as the measurement matrix in order to decrease the computational complexity; and rebinning of the projections to parallel rays in order to extend its application to fan beam and helical cone beam scans. The weight involved in the proposed weighted CS model, denoted by Error Adaptation Weight (EAW), is calculated based on the statistical characteristics of CT reconstruction and is a function of Poisson measurement noise and rebinning interpolation error. Simulation results show that low computational complexity of the proposed method made the fast recovery of the CT images possible and using EAW reduces the reconstruction error by one order of magnitude. Recovery of a high quality 512$\times$ 512 image was achieved in less than 20 sec on a desktop computer without numerical optimizations.

Efficient unimodality test in clustering by signature testing

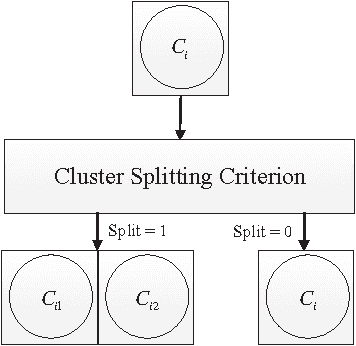
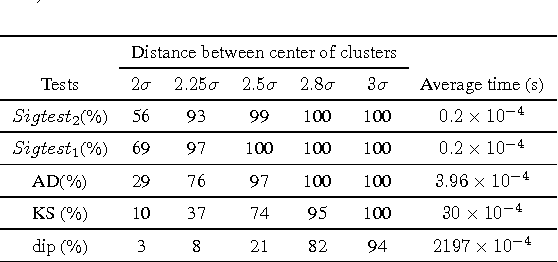
This paper provides a new unimodality test with application in hierarchical clustering methods. The proposed method denoted by signature test (Sigtest), transforms the data based on its statistics. The transformed data has much smaller variation compared to the original data and can be evaluated in a simple proposed unimodality test. Compared with the existing unimodality tests, Sigtest is more accurate in detecting the overlapped clusters and has a much less computational complexity. Simulation results demonstrate the efficiency of this statistic test for both real and synthetic data sets.

Noise Invalidation Denoising

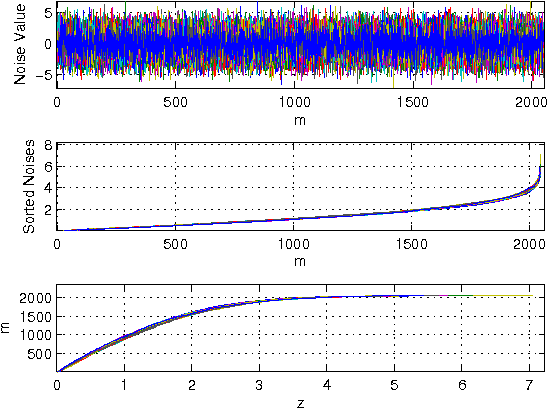
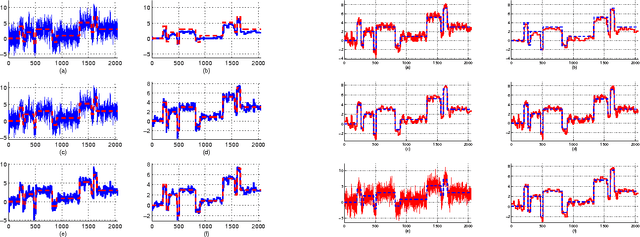
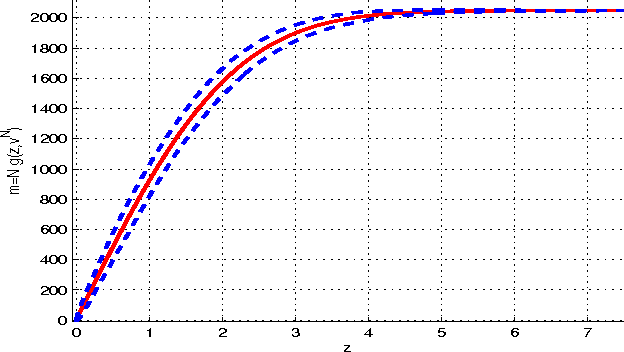
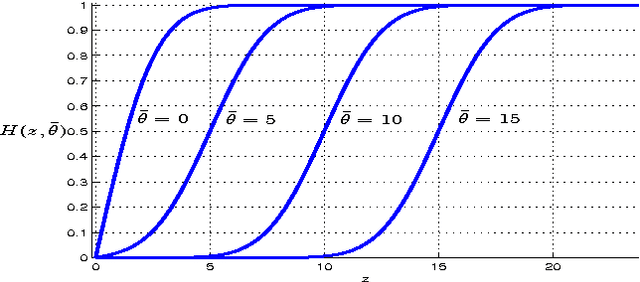
A denoising technique based on noise invalidation is proposed. The adaptive approach derives a noise signature from the noise order statistics and utilizes the signature to denoise the data. The novelty of this approach is in presenting a general-purpose denoising in the sense that it does not need to employ any particular assumption on the structure of the noise-free signal, such as data smoothness or sparsity of the coefficients. An advantage of the method is in denoising the corrupted data in any complete basis transformation (orthogonal or non-orthogonal). Experimental results show that the proposed method, called Noise Invalidation Denoising (NIDe), outperforms existing denoising approaches in terms of Mean Square Error (MSE).