A New Tightly-Coupled Dual-VIO for a Mobile Manipulator With Dynamic Locomotion

This paper introduces a new dual monocular visualinertial odometry (dual-VIO) strategy for a mobile manipulator operating under dynamic locomotion, i.e. coordinated movement involving both the base platform and the manipulator arm. Our approach has been motivated by challenges arising from inaccurate estimation due to coupled excitation when the mobile manipulator is engaged in dynamic locomotion in cluttered environments. The technique maintains two independent monocular VIO modules, with one at the mobile base and the other at the end-effector (EE), which are tightly coupled at the low level of the factor graph. The proposed method treats each monocular VIO with respect to each other as a positional anchor through arm-kinematics. These anchor points provide a soft geometric constraint during the VIO pose optimization. This allows us to stabilize both estimators in case of instability of one estimator in highly dynamic locomotions. The performance of our approach has been demonstrated through extensive experimental testing with a mobile manipulator tested in comparison to running dual VINS-Mono in parallel. We envision that our method can also provide a foundation towards active-SLAM (ASLAM) with a new perspective on multi-VIO fusion and system redundancy.

End-Effector Stabilization of a 10-DOF Mobile Manipulator using Nonlinear Model Predictive Control

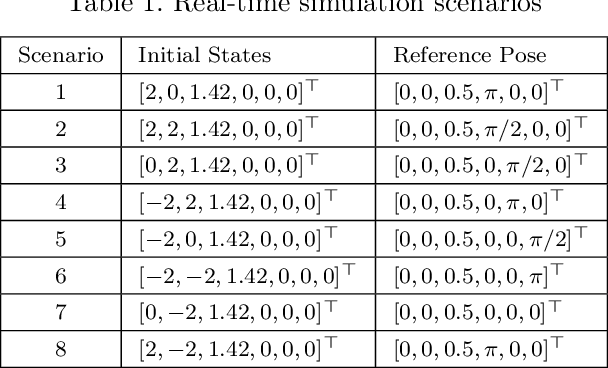
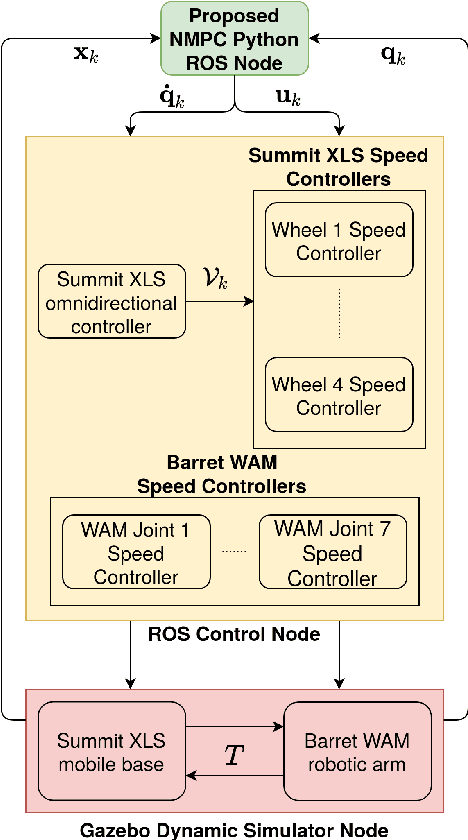
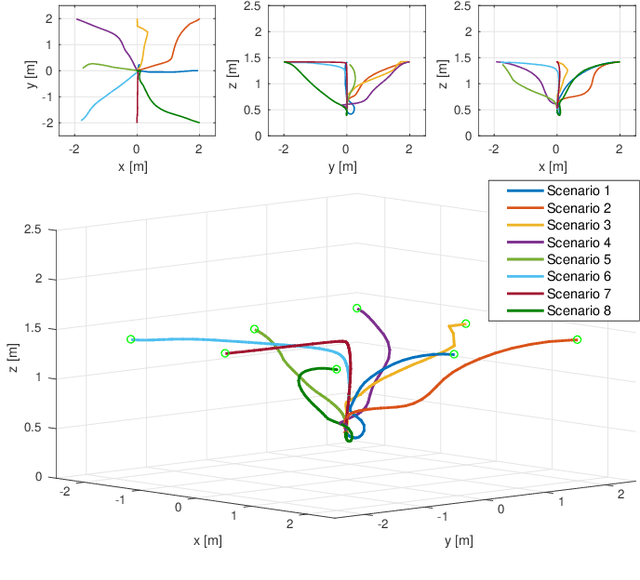
Motion control of mobile manipulators (a robotic arm mounted on a mobile base) can be challenging for complex tasks such as material and package handling. In this paper, a task-space stabilization controller based on Nonlinear Model Predictive Control (NMPC) is designed and implemented to a 10 Degrees of Freedom (DOF) mobile manipulator which consists of a 7-DOF robotic arm and a 3-DOF mobile base. The system model is based on kinematic models where the end-effector orientation is parameterized directly by a rotation matrix. The state and control constraints as well as singularity constraints are explicitly included in the NMPC formulation. The controller is tested using real-time simulations, which demonstrate high positioning accuracy with tractable computational cost.