Thinking About Causation: A Causal Language with Epistemic Operators

This paper proposes a formal framework for modeling the interaction of causal and (qualitative) epistemic reasoning. To this purpose, we extend the notion of a causal model with a representation of the epistemic state of an agent. On the side of the object language, we add operators to express knowledge and the act of observing new information. We provide a sound and complete axiomatization of the logic, and discuss the relation of this framework to causal team semantics.

Learning Probabilities: Towards a Logic of Statistical Learning

We propose a new model for forming beliefs and learning about unknown probabilities (such as the probability of picking a red marble from a bag with an unknown distribution of coloured marbles). The most widespread model for such situations of 'radical uncertainty' is in terms of imprecise probabilities, i.e. representing the agent's knowledge as a set of probability measures. We add to this model a plausibility map, associating to each measure a plausibility number, as a way to go beyond what is known with certainty and represent the agent's beliefs about probability. There are a number of standard examples: Shannon Entropy, Centre of Mass etc. We then consider learning of two types of information: (1) learning by repeated sampling from the unknown distribution (e.g. picking marbles from the bag); and (2) learning higher-order information about the distribution (in the shape of linear inequalities, e.g. we are told there are more red marbles than green marbles). The first changes only the plausibility map (via a 'plausibilistic' version of Bayes' Rule), but leaves the given set of measures unchanged; the second shrinks the set of measures, without changing their plausibility. Beliefs are defined as in Belief Revision Theory, in terms of truth in the most plausible worlds. But our belief change does not comply with standard AGM axioms, since the revision induced by (1) is of a non-AGM type. This is essential, as it allows our agents to learn the true probability: we prove that the beliefs obtained by repeated sampling converge almost surely to the correct belief (in the true probability). We end by sketching the contours of a dynamic doxastic logic for statistical learning.

Argument-based Belief in Topological Structures

This paper combines two studies: a topological semantics for epistemic notions and abstract argumentation theory. In our combined setting, we use a topological semantics to represent the structure of an agent's collection of evidence, and we use argumentation theory to single out the relevant sets of evidence through which a notion of beliefs grounded on arguments is defined. We discuss the formal properties of this newly defined notion, providing also a formal language with a matching modality together with a sound and complete axiom system for it. Despite the fact that our agent can combine her evidence in a 'rational' way (captured via the topological structure), argument-based beliefs are not closed under conjunction. This illustrates the difference between an agent's reasoning abilities (i.e. the way she is able to combine her available evidence) and the closure properties of her beliefs. We use this point to argue for why the failure of closure under conjunction of belief should not bear the burden of the failure of rationality.

On the Solvability of Inductive Problems: A Study in Epistemic Topology

We investigate the issues of inductive problem-solving and learning by doxastic agents. We provide topological characterizations of solvability and learnability, and we use them to prove that AGM-style belief revision is "universal", i.e., that every solvable problem is solvable by AGM conditioning.

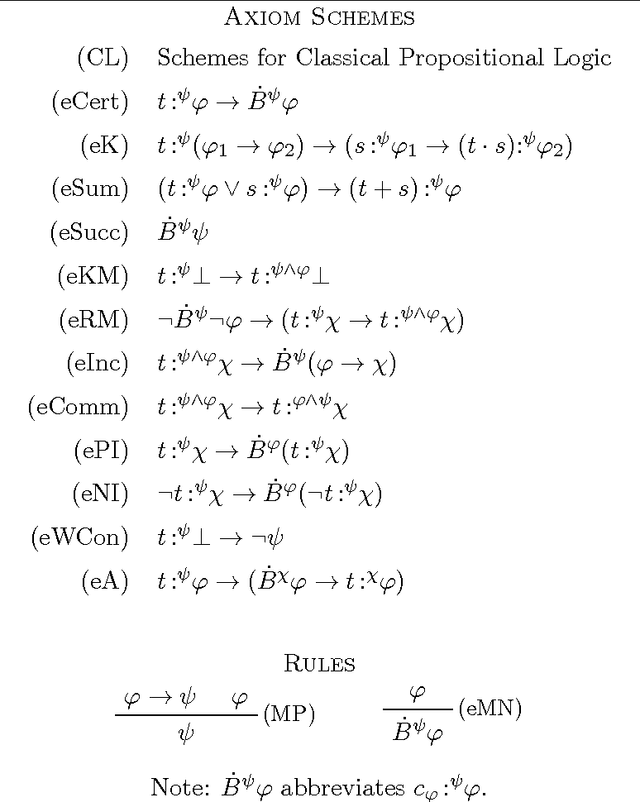
Revisable Justified Belief: Preliminary Report

The theory $\mathsf{CDL}$ of Conditional Doxastic Logic is the single-agent version of Board's multi-agent theory $\mathsf{BRSIC}$ of conditional belief. $\mathsf{CDL}$ may be viewed as a version of AGM belief revision theory in which Boolean combinations of revisions are expressible in the language. We introduce a theory $\mathsf{JCDL}$ of Justified Conditional Doxastic Logic that replaces conditional belief formulas $B^\psi\varphi$ by expressions $t{\,:^{\psi}}\varphi$ made up of a term $t$ whose syntactic structure suggests a derivation of the belief $\varphi$ after revision by $\psi$. This allows us to think of terms $t$ as reasons justifying a belief in various formulas after a revision takes place. We show that $\mathsf{JCDL}$-theorems are the exact analogs of $\mathsf{CDL}$-theorems, and that this result holds the other way around as well. This allows us to think of $\mathsf{JCDL}$ as a theory of revisable justified belief.