Revisable Justified Belief: Preliminary Report
Paper and Code
Mar 27, 2015


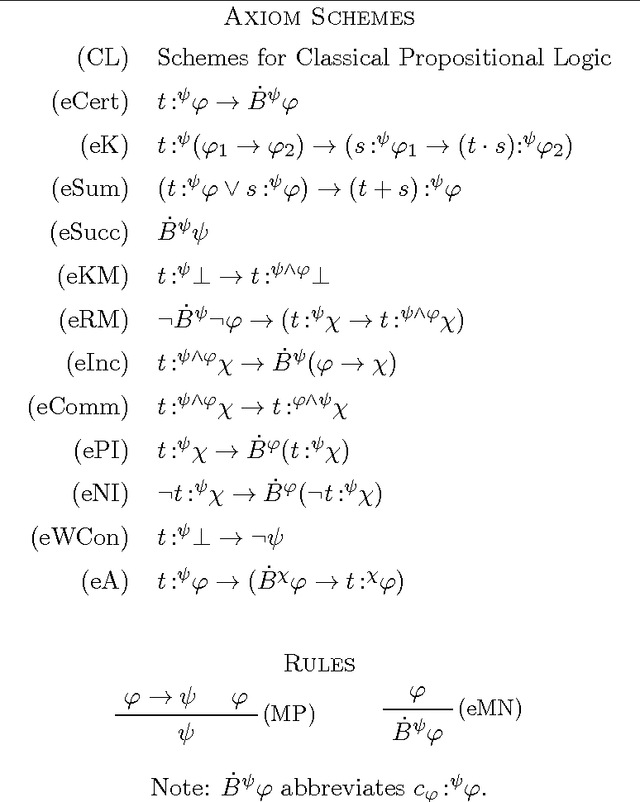
The theory $\mathsf{CDL}$ of Conditional Doxastic Logic is the single-agent version of Board's multi-agent theory $\mathsf{BRSIC}$ of conditional belief. $\mathsf{CDL}$ may be viewed as a version of AGM belief revision theory in which Boolean combinations of revisions are expressible in the language. We introduce a theory $\mathsf{JCDL}$ of Justified Conditional Doxastic Logic that replaces conditional belief formulas $B^\psi\varphi$ by expressions $t{\,:^{\psi}}\varphi$ made up of a term $t$ whose syntactic structure suggests a derivation of the belief $\varphi$ after revision by $\psi$. This allows us to think of terms $t$ as reasons justifying a belief in various formulas after a revision takes place. We show that $\mathsf{JCDL}$-theorems are the exact analogs of $\mathsf{CDL}$-theorems, and that this result holds the other way around as well. This allows us to think of $\mathsf{JCDL}$ as a theory of revisable justified belief.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge