Knowledge, Justification, and Reason-Based Belief

Is knowledge definable as justified true belief ("JTB")? We argue that one can legitimately answer positively or negatively, depending on how the notion of justification is understood. To facilitate our argument, we introduce a simple propositional logic of reason-based belief. We show that this logic is sufficiently flexible to accommodate various useful features, including quantification over reasons. We use our framework to contrast two notions of JTB: one internalist, the other externalist. We argue that Gettier cases essentially challenge the internalist notion but not the externalist one. In particular, we may equate knowledge and JTB if the latter is grounded in what we call "adequate" reasons.

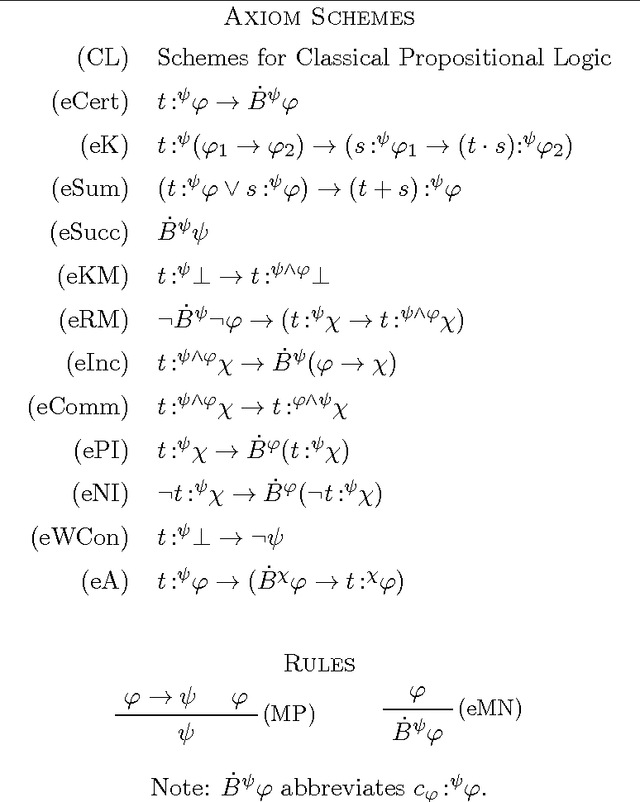
Revisable Justified Belief: Preliminary Report

The theory $\mathsf{CDL}$ of Conditional Doxastic Logic is the single-agent version of Board's multi-agent theory $\mathsf{BRSIC}$ of conditional belief. $\mathsf{CDL}$ may be viewed as a version of AGM belief revision theory in which Boolean combinations of revisions are expressible in the language. We introduce a theory $\mathsf{JCDL}$ of Justified Conditional Doxastic Logic that replaces conditional belief formulas $B^\psi\varphi$ by expressions $t{\,:^{\psi}}\varphi$ made up of a term $t$ whose syntactic structure suggests a derivation of the belief $\varphi$ after revision by $\psi$. This allows us to think of terms $t$ as reasons justifying a belief in various formulas after a revision takes place. We show that $\mathsf{JCDL}$-theorems are the exact analogs of $\mathsf{CDL}$-theorems, and that this result holds the other way around as well. This allows us to think of $\mathsf{JCDL}$ as a theory of revisable justified belief.

Belief as Willingness to Bet

We investigate modal logics of high probability having two unary modal operators: an operator $K$ expressing probabilistic certainty and an operator $B$ expressing probability exceeding a fixed rational threshold $c\geq\frac 12$. Identifying knowledge with the former and belief with the latter, we may think of $c$ as the agent's betting threshold, which leads to the motto "belief is willingness to bet." The logic $\mathsf{KB.5}$ for $c=\frac 12$ has an $\mathsf{S5}$ $K$ modality along with a sub-normal $B$ modality that extends the minimal modal logic $\mathsf{EMND45}$ by way of four schemes relating $K$ and $B$, one of which is a complex scheme arising out of a theorem due to Scott. Lenzen was the first to use Scott's theorem to show that a version of this logic is sound and complete for the probability interpretation. We reformulate Lenzen's results and present them here in a modern and accessible form. In addition, we introduce a new epistemic neighborhood semantics that will be more familiar to modern modal logicians. Using Scott's theorem, we provide the Lenzen-derivative properties that must be imposed on finite epistemic neighborhood models so as to guarantee the existence of a probability measure respecting the neighborhood function in the appropriate way for threshold $c=\frac 12$. This yields a link between probabilistic and modal neighborhood semantics that we hope will be of use in future work on modal logics of qualitative probability. We leave open the question of which properties must be imposed on finite epistemic neighborhood models so as to guarantee existence of an appropriate probability measure for thresholds $c\neq\frac 12$.

Logics of Temporal-Epistemic Actions

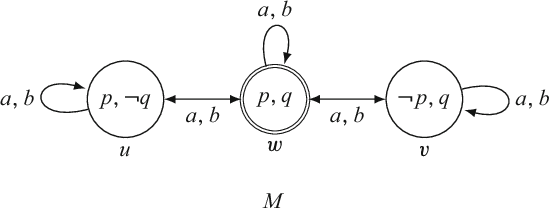
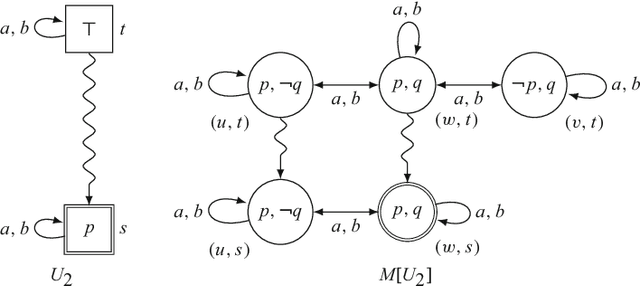
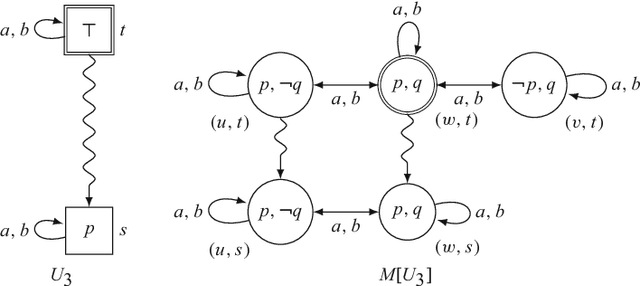
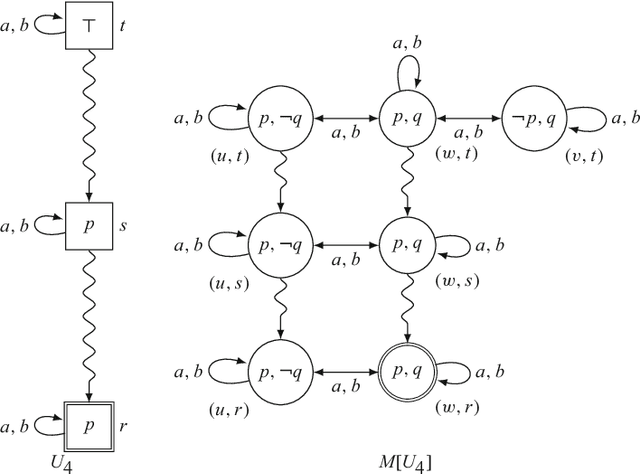
We present Dynamic Epistemic Temporal Logic, a framework for reasoning about operations on multi-agent Kripke models that contain a designated temporal relation. These operations are natural extensions of the well-known "action models" from Dynamic Epistemic Logic. Our "temporal action models" may be used to define a number of informational actions that can modify the "objective" temporal structure of a model along with the agents' basic and higher-order knowledge and beliefs about this structure, including their beliefs about the time. In essence, this approach provides one way to extend the domain of action model-style operations from atemporal Kripke models to temporal Kripke models in a manner that allows actions to control the flow of time. We present a number of examples to illustrate the subtleties involved in interpreting the effects of our extended action models on temporal Kripke models. We also study preservation of important epistemic-temporal properties of temporal Kripke models under temporal action model-induced operations, provide complete axiomatizations for two theories of temporal action models, and connect our approach with previous work on time in Dynamic Epistemic Logic.