Somayeh Danafar
Kernel-based Information Criterion
Dec 15, 2014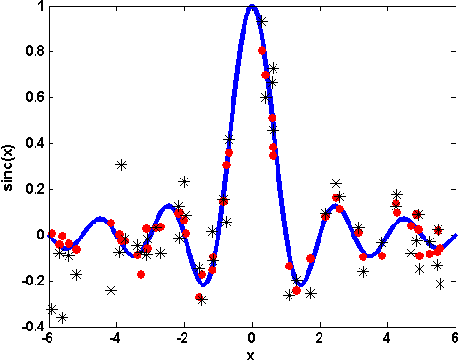
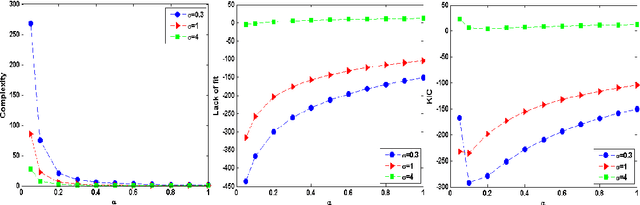
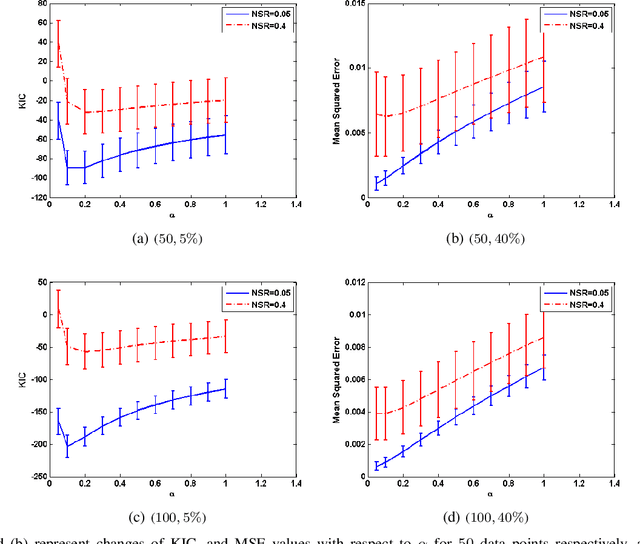
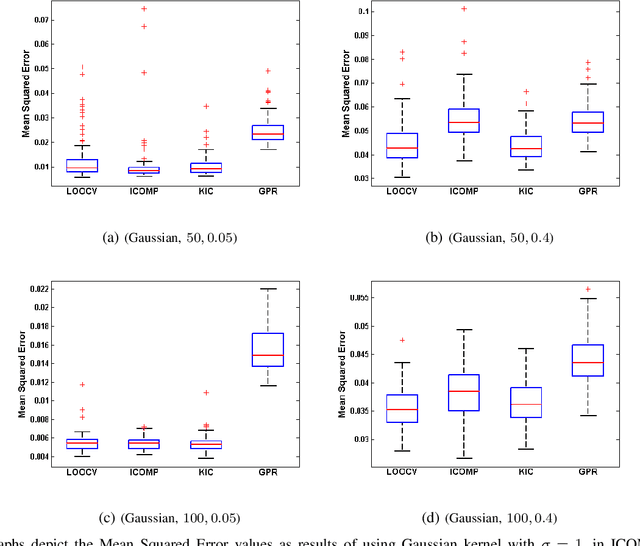
Abstract:This paper introduces Kernel-based Information Criterion (KIC) for model selection in regression analysis. The novel kernel-based complexity measure in KIC efficiently computes the interdependency between parameters of the model using a variable-wise variance and yields selection of better, more robust regressors. Experimental results show superior performance on both simulated and real data sets compared to Leave-One-Out Cross-Validation (LOOCV), kernel-based Information Complexity (ICOMP), and maximum log of marginal likelihood in Gaussian Process Regression (GPR).
Testing Hypotheses by Regularized Maximum Mean Discrepancy
May 02, 2013



Abstract:Do two data samples come from different distributions? Recent studies of this fundamental problem focused on embedding probability distributions into sufficiently rich characteristic Reproducing Kernel Hilbert Spaces (RKHSs), to compare distributions by the distance between their embeddings. We show that Regularized Maximum Mean Discrepancy (RMMD), our novel measure for kernel-based hypothesis testing, yields substantial improvements even when sample sizes are small, and excels at hypothesis tests involving multiple comparisons with power control. We derive asymptotic distributions under the null and alternative hypotheses, and assess power control. Outstanding results are obtained on: challenging EEG data, MNIST, the Berkley Covertype, and the Flare-Solar dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge