Addressing Mark Imbalance in Integration-free Neural Marked Temporal Point Processes

Marked Temporal Point Process (MTPP) has been well studied to model the event distribution in marked event streams, which can be used to predict the mark and arrival time of the next event. However, existing studies overlook that the distribution of event marks is highly imbalanced in many real-world applications, with some marks being frequent but others rare. The imbalance poses a significant challenge to the performance of the next event prediction, especially for events of rare marks. To address this issue, we propose a thresholding method, which learns thresholds to tune the mark probability normalized by the mark's prior probability to optimize mark prediction, rather than predicting the mark directly based on the mark probability as in existing studies. In conjunction with this method, we predict the mark first and then the time. In particular, we develop a novel neural MTPP model to support effective time sampling and estimation of mark probability without computationally expensive numerical improper integration. Extensive experiments on real-world datasets demonstrate the superior performance of our solution against various baselines for the next event mark and time prediction. The code is available at https://github.com/undes1red/IFNMTPP.

Explainable History Distillation by Marked Temporal Point Process

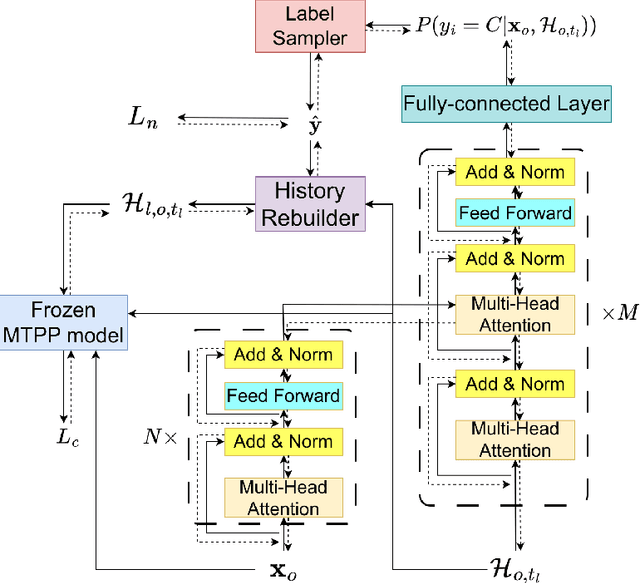
Explainability of machine learning models is mandatory when researchers introduce these commonly believed black boxes to real-world tasks, especially high-stakes ones. In this paper, we build a machine learning system to automatically generate explanations of happened events from history by \gls{ca} based on the \acrfull{tpp}. Specifically, we propose a new task called \acrfull{ehd}. This task requires a model to distill as few events as possible from observed history. The target is that the event distribution conditioned on left events predicts the observed future noticeably worse. We then regard distilled events as the explanation for the future. To efficiently solve \acrshort{ehd}, we rewrite the task into a \gls{01ip} and directly estimate the solution to the program by a model called \acrfull{model}. This work fills the gap between our task and existing works, which only spot the difference between factual and counterfactual worlds after applying a predefined modification to the environment. Experiment results on Retweet and StackOverflow datasets prove that \acrshort{model} significantly outperforms other \acrshort{ehd} baselines and can reveal the rationale underpinning real-world processes.

Intensity-free Integral-based Learning of Marked Temporal Point Processes

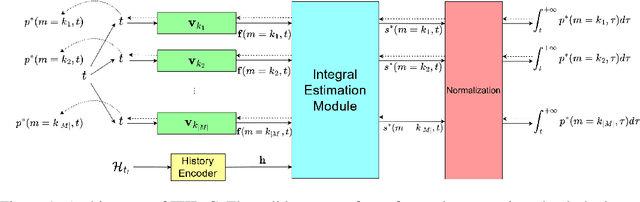
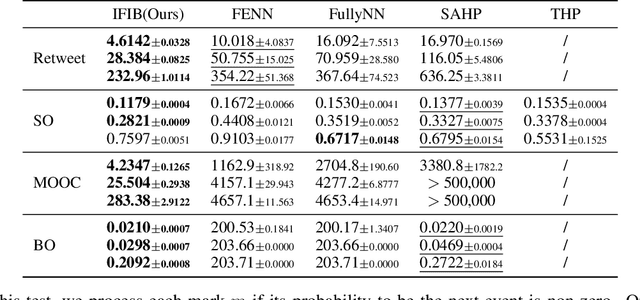
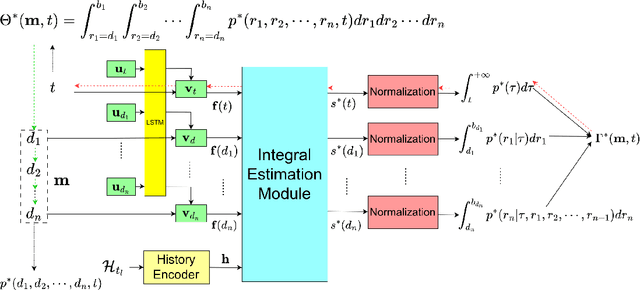
In the marked temporal point processes (MTPP), a core problem is to parameterize the conditional joint PDF (probability distribution function) $p^*(m,t)$ for inter-event time $t$ and mark $m$, conditioned on the history. The majority of existing studies predefine intensity functions. Their utility is challenged by specifying the intensity function's proper form, which is critical to balance expressiveness and processing efficiency. Recently, there are studies moving away from predefining the intensity function -- one models $p^*(t)$ and $p^*(m)$ separately, while the other focuses on temporal point processes (TPPs), which do not consider marks. This study aims to develop high-fidelity $p^*(m,t)$ for discrete events where the event marks are either categorical or numeric in a multi-dimensional continuous space. We propose a solution framework IFIB (\underline{I}ntensity-\underline{f}ree \underline{I}ntegral-\underline{b}ased process) that models conditional joint PDF $p^*(m,t)$ directly without intensity functions. It remarkably simplifies the process to compel the essential mathematical restrictions. We show the desired properties of IFIB and the superior experimental results of IFIB on real-world and synthetic datasets. The code is available at \url{https://github.com/StepinSilence/IFIB}.