Simone Bassis
Department of Computer Science - University of Milano, Italy
Semi-structured data extraction and modelling: the WIA Project
Sep 30, 2013

Abstract:Over the last decades, the amount of data of all kinds available electronically has increased dramatically. Data are accessible through a range of interfaces including Web browsers, database query languages, application-specific interfaces, built on top of a number of different data exchange formats. All these data span from un-structured to highly structured data. Very often, some of them have structure even if the structure is implicit, and not as rigid or regular as that found in standard database systems. Spreadsheet documents are prototypical in this respect. Spreadsheets are the lightweight technology able to supply companies with easy to build business management and business intelligence applications, and business people largely adopt spreadsheets as smart vehicles for data files generation and sharing. Actually, the more spreadsheets grow in complexity (e.g., their use in product development plans and quoting), the more their arrangement, maintenance, and analysis appear as a knowledge-driven activity. The algorithmic approach to the problem of automatic data structure extraction from spreadsheet documents (i.e., grid-structured and free topological-related data) emerges from the WIA project: Worksheets Intelligent Analyser. The WIA-algorithm shows how to provide a description of spreadsheet contents in terms of higher level of abstractions or conceptualisations. In particular, the WIA-algorithm target is about the extraction of i) the calculus work-flow implemented in the spreadsheets formulas and ii) the logical role played by the data which take part into the calculus. The aim of the resulting conceptualisations is to provide spreadsheets with abstract representations useful for further model refinements and optimizations through evolutionary algorithms computations.
* In Proceedings Wivace 2013, arXiv:1309.7122
DANCo: Dimensionality from Angle and Norm Concentration
Jun 18, 2012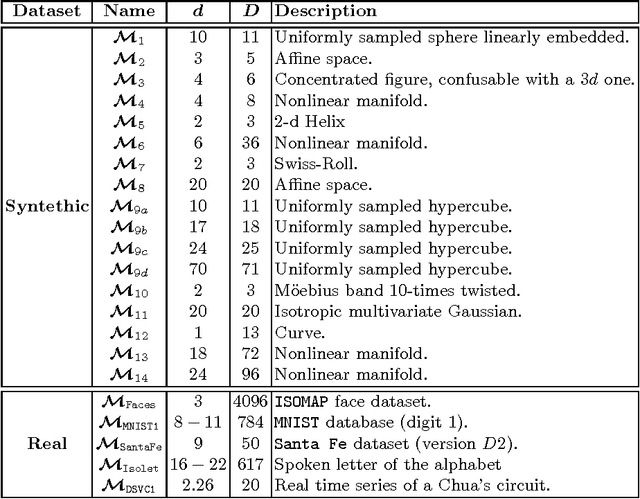
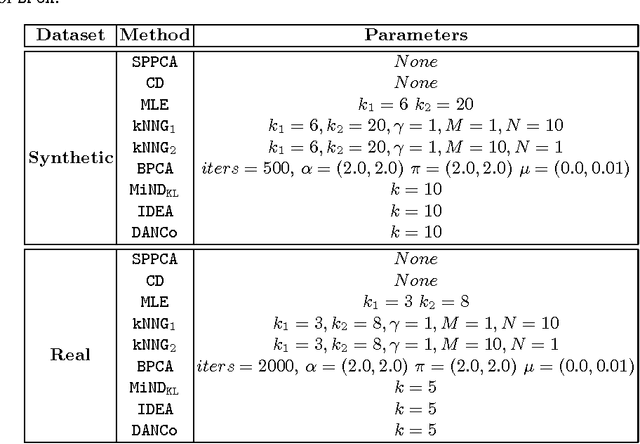
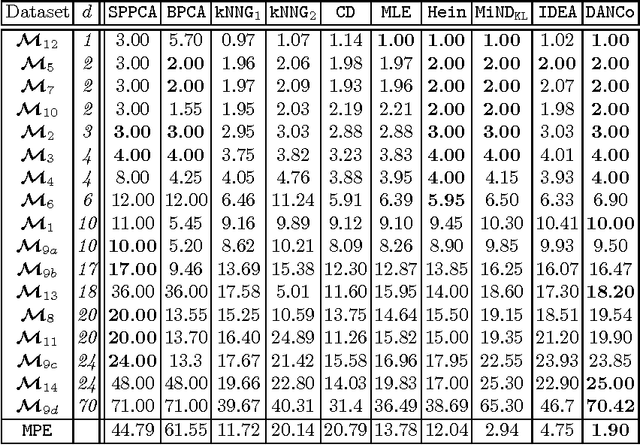
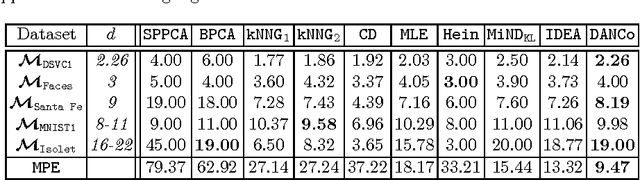
Abstract:In the last decades the estimation of the intrinsic dimensionality of a dataset has gained considerable importance. Despite the great deal of research work devoted to this task, most of the proposed solutions prove to be unreliable when the intrinsic dimensionality of the input dataset is high and the manifold where the points lie is nonlinearly embedded in a higher dimensional space. In this paper we propose a novel robust intrinsic dimensionality estimator that exploits the twofold complementary information conveyed both by the normalized nearest neighbor distances and by the angles computed on couples of neighboring points, providing also closed-forms for the Kullback-Leibler divergences of the respective distributions. Experiments performed on both synthetic and real datasets highlight the robustness and the effectiveness of the proposed algorithm when compared to state of the art methodologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge