TINYCD: A Deep Learning Model For Change Detection

The aim of change detection (CD) is to detect changes occurred in the same area by comparing two images of that place taken at different times. The challenging part of the CD is to keep track of the changes the user wants to highlight, such as new buildings, and to ignore changes due to external factors such as environmental, lighting condition, fog or seasonal changes. Recent developments in the field of deep learning enabled researchers to achieve outstanding performance in this area. In particular, different mechanisms of space-time attention allowed to exploit the spatial features that are extracted from the models and to correlate them also in a temporal way by exploiting both the available images. The downside is that the models have become increasingly complex and large, often unfeasible for edge applications. These are limitations when the models must be applied to the industrial field or in applications requiring real-time performances. In this work we propose a novel model, called TinyCD, demonstrating to be both lightweight and effective, able to achieve performances comparable or even superior to the current state of the art with 13-150X fewer parameters. In our approach we have exploited the importance of low-level features to compare images. To do this, we use only few backbone blocks. This strategy allow us to keep the number of network parameters low. To compose the features extracted from the two images, we introduce a novel, economical in terms of parameters, mixing block capable of cross correlating features in both space and time domains. Finally, to fully exploit the information contained in the computed features, we define the PW-MLP block able to perform a pixel wise classification. Source code, models and results are available here: https://github.com/AndreaCodegoni/Tiny_model_4_CD

DANCo: Dimensionality from Angle and Norm Concentration

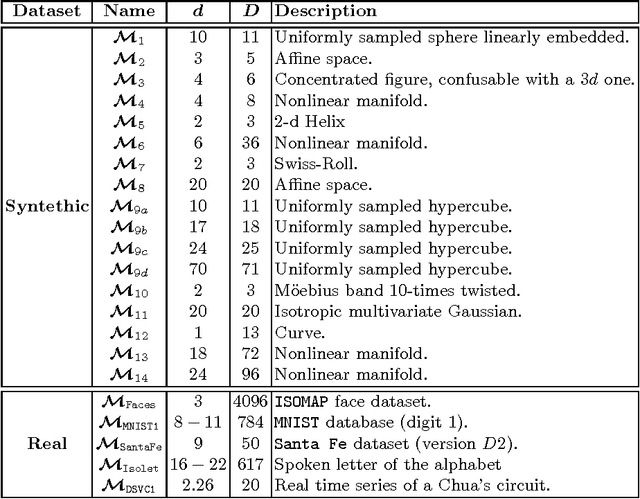
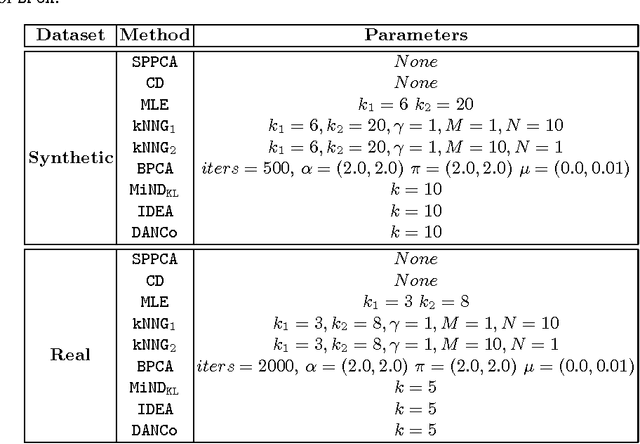
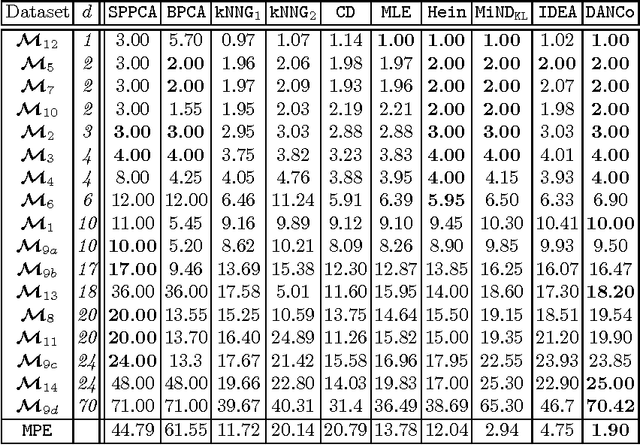
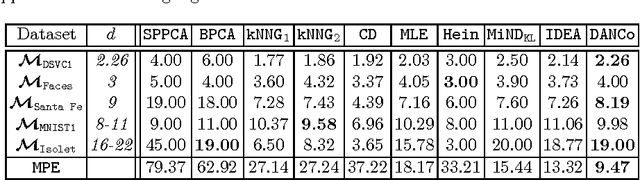
In the last decades the estimation of the intrinsic dimensionality of a dataset has gained considerable importance. Despite the great deal of research work devoted to this task, most of the proposed solutions prove to be unreliable when the intrinsic dimensionality of the input dataset is high and the manifold where the points lie is nonlinearly embedded in a higher dimensional space. In this paper we propose a novel robust intrinsic dimensionality estimator that exploits the twofold complementary information conveyed both by the normalized nearest neighbor distances and by the angles computed on couples of neighboring points, providing also closed-forms for the Kullback-Leibler divergences of the respective distributions. Experiments performed on both synthetic and real datasets highlight the robustness and the effectiveness of the proposed algorithm when compared to state of the art methodologies.