Incremental Inference on Higher-Order Probabilistic Graphical Models Applied to Constraint Satisfaction Problems

Probabilistic graphical models (PGMs) are tools for solving complex probabilistic relationships. However, suboptimal PGM structures are primarily used in practice. This dissertation presents three contributions to the PGM literature. The first is a comparison between factor graphs and cluster graphs on graph colouring problems such as Sudokus - indicating a significant advantage for preferring cluster graphs. The second is an application of cluster graphs to a practical problem in cartography: land cover classification boosting. The third is a PGMs formulation for constraint satisfaction problems and an algorithm called purge-and-merge to solve such problems too complex for traditional PGMs.

A Probabilistic Graphical Model Approach to the Structure-and-Motion Problem

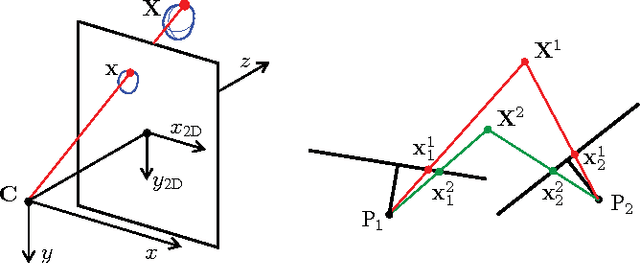
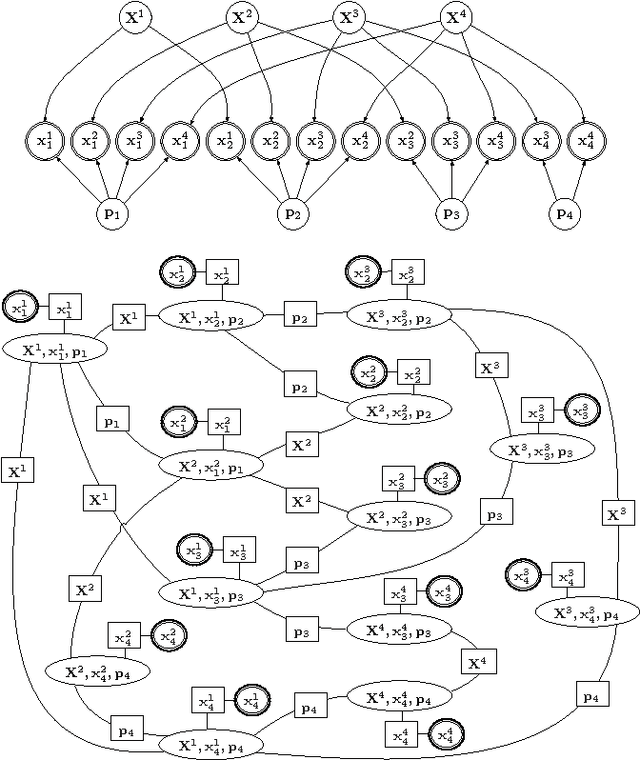
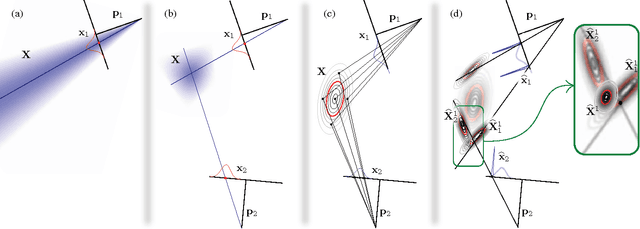
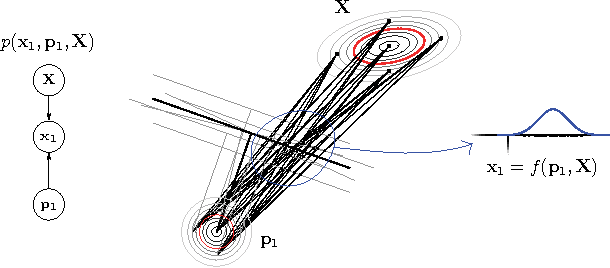
We present a means of formulating and solving the well known structure-and-motion problem in computer vision with probabilistic graphical models. We model the unknown camera poses and 3D feature coordinates as well as the observed 2D projections as Gaussian random variables, using sigma point parameterizations to effectively linearize the nonlinear relationships between these variables. Those variables involved in every projection are grouped into a cluster, and we connect the clusters in a cluster graph. Loopy belief propagation is performed over this graph, in an iterative re-initialization and estimation procedure, and we find that our approach shows promise in both simulation and on real-world data. The PGM is easily extendable to include additional parameters or constraints.

Graph Coloring: Comparing Cluster Graphs to Factor Graphs

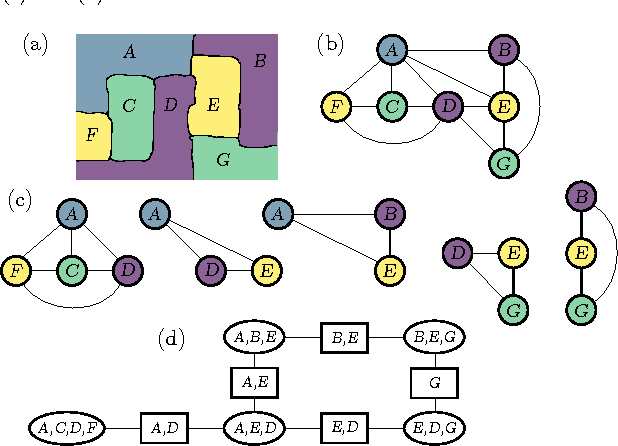
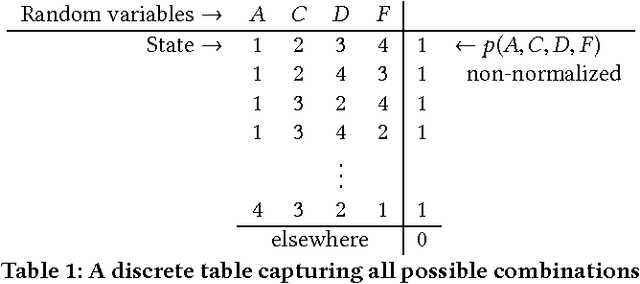
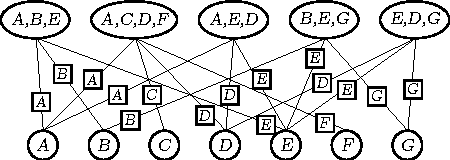
We present a means of formulating and solving graph coloring problems with probabilistic graphical models. In contrast to the prevalent literature that uses factor graphs for this purpose, we instead approach it from a cluster graph perspective. Since there seems to be a lack of algorithms to automatically construct valid cluster graphs, we provide such an algorithm (termed LTRIP). Our experiments indicate a significant advantage for preferring cluster graphs over factor graphs, both in terms of accuracy as well as computational efficiency.

Strengthening Probabilistic Graphical Models: The Purge-and-merge Algorithm

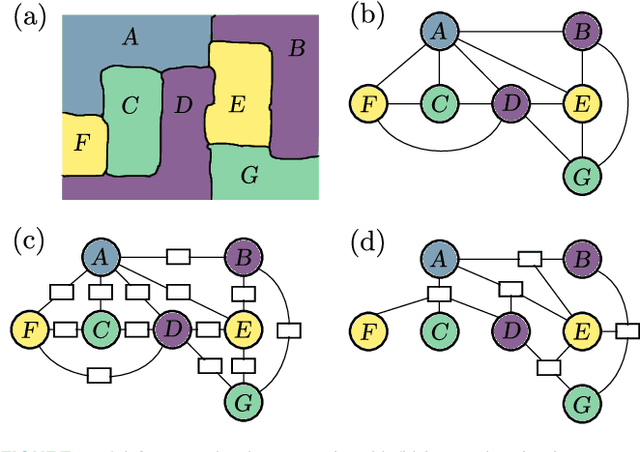
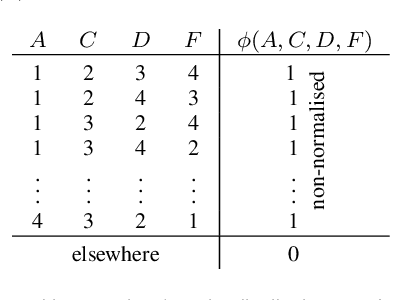
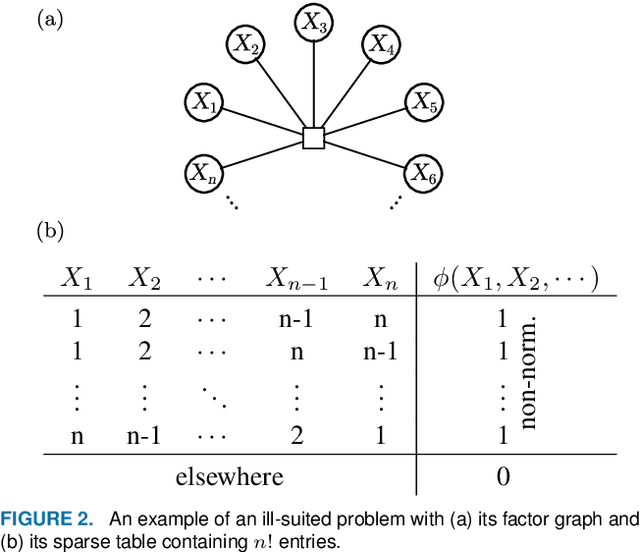
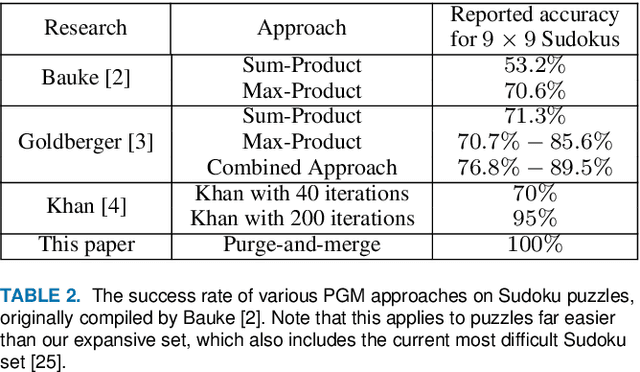
Probabilistic graphical models (PGMs) are powerful tools for solving systems of complex relationships over a variety of probability distributions. Tree-structured PGMs always result in efficient and exact solutions, while inference on graph (or loopy) structured PGMs is not guaranteed to discover the optimal solutions. It is in principle possible to convert loopy PGMs to an equivalent tree structure, but for most interesting problems this is impractical due to exponential blow-up. To address this, we developed the purge-and-merge algorithm. The idea behind this algorithm is to iteratively nudge a malleable graph structure towards a tree structure by selectively merging factors. The merging process is designed to avoid exponential blow-up by making use of sparse structures from which redundancy is purged as the algorithm progresses. This approach is evaluated on a number of constraint-satisfaction puzzles such as Sudoku, Fill-a-pix, and Kakuro. On these tasks, our system outperformed other PGM-based approaches reported in the literature. Although these tasks were limited to the binary logic of CSP, we believe it holds promise for extension to general PGM inference.

Plant-wide fault and disturbance screening using combined transfer entropy and eigenvector centrality analysis

Finding the source of a disturbance or fault in complex systems such as industrial chemical processing plants can be a difficult task and consume a significant number of engineering hours. In many cases, a systematic elimination procedure is considered to be the only feasible approach but can cause undesired process upsets. Practitioners desire robust alternative approaches. This paper presents an unsupervised, data-driven method for ranking process elements according to the magnitude and novelty of their influence. Partial bivariate transfer entropy estimation is used to infer a weighted directed graph of process elements. Eigenvector centrality is applied to rank network nodes according to their overall effect. As the ranking of process elements rely on emerging properties that depend on the aggregate of many connections, the results are robust to errors in the estimation of individual edge properties and the inclusion of indirect connections that do not represent the true causal structure of the process. A monitoring chart of continuously calculated process element importance scores over multiple overlapping time regions can assist with incipient fault detection. Ranking results combined with visual inspection of information transfer networks is also useful for root cause analysis of known faults and disturbances. A software implementation of the proposed method is available.