Strengthening Probabilistic Graphical Models: The Purge-and-merge Algorithm

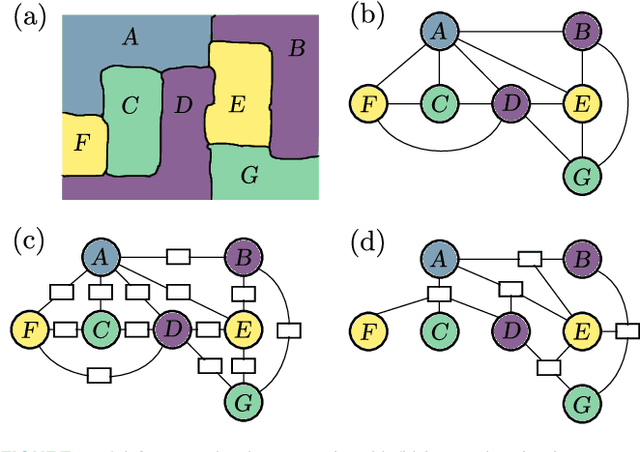
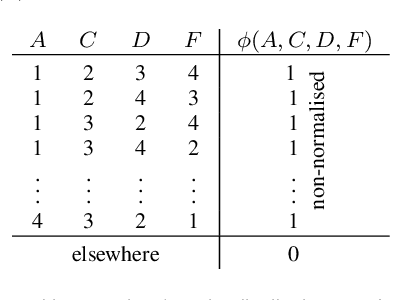
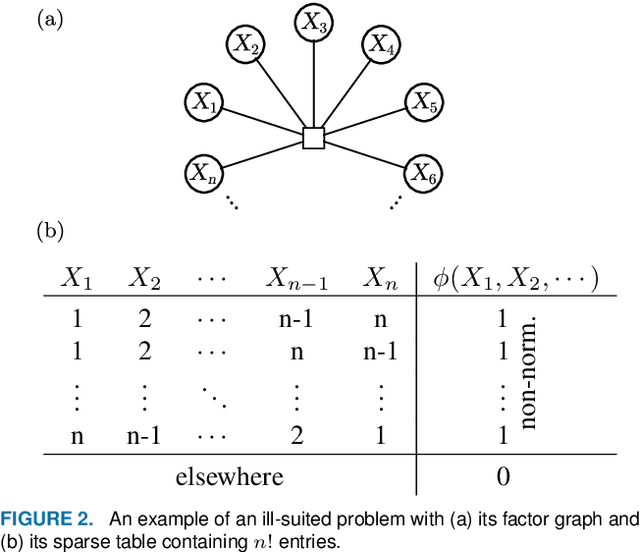
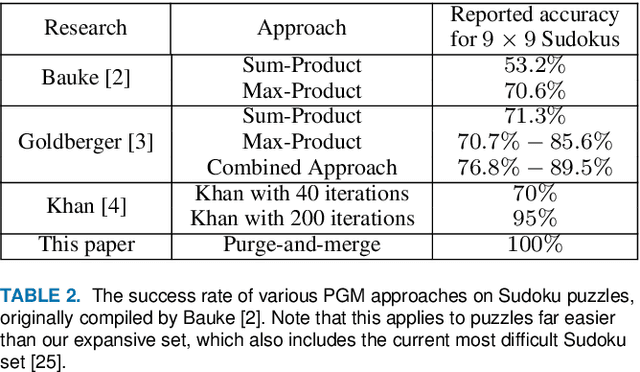
Probabilistic graphical models (PGMs) are powerful tools for solving systems of complex relationships over a variety of probability distributions. Tree-structured PGMs always result in efficient and exact solutions, while inference on graph (or loopy) structured PGMs is not guaranteed to discover the optimal solutions. It is in principle possible to convert loopy PGMs to an equivalent tree structure, but for most interesting problems this is impractical due to exponential blow-up. To address this, we developed the purge-and-merge algorithm. The idea behind this algorithm is to iteratively nudge a malleable graph structure towards a tree structure by selectively merging factors. The merging process is designed to avoid exponential blow-up by making use of sparse structures from which redundancy is purged as the algorithm progresses. This approach is evaluated on a number of constraint-satisfaction puzzles such as Sudoku, Fill-a-pix, and Kakuro. On these tasks, our system outperformed other PGM-based approaches reported in the literature. Although these tasks were limited to the binary logic of CSP, we believe it holds promise for extension to general PGM inference.