SHREC 2025: Protein surface shape retrieval including electrostatic potential

This SHREC 2025 track dedicated to protein surface shape retrieval involved 9 participating teams. We evaluated the performance in retrieval of 15 proposed methods on a large dataset of 11,555 protein surfaces with calculated electrostatic potential (a key molecular surface descriptor). The performance in retrieval of the proposed methods was evaluated through different metrics (Accuracy, Balanced accuracy, F1 score, Precision and Recall). The best retrieval performance was achieved by the proposed methods that used the electrostatic potential complementary to molecular surface shape. This observation was also valid for classes with limited data which highlights the importance of taking into account additional molecular surface descriptors.

Recognising geometric primitives in 3D point clouds of mechanical CAD objects

The problem faced in this paper concerns the recognition of simple and complex geometric primitives in point clouds resulting from scans of mechanical CAD objects. A large number of points, the presence of noise, outliers, missing or redundant parts and uneven distribution are the main problems to be addressed to meet this need. In this article we propose a solution, based on the Hough transform, that can recognize simple and complex geometric primitives and is robust to noise, outliers, and missing parts. Additionally, we can extract a series of geometric descriptors that uniquely characterize a primitive and, based on them, aggregate the output into maximal or compound primitives, thus reducing oversegmentation. The results presented in the paper demonstrate the robustness of the method and its competitiveness with respect to other solutions proposed in the literature.

Fitting and recognition of geometric primitives in segmented 3D point clouds using a localized voting procedure

The automatic creation of geometric models from point clouds has numerous applications in CAD (e.g., reverse engineering, manufacturing, assembling) and, more in general, in shape modelling and processing. Given a segmented point cloud representing a man-made object, we propose a method for recognizing simple geometric primitives and their interrelationships. Our approach is based on the Hough transform (HT) for its ability to deal with noise, missing parts and outliers. In our method we introduce a novel technique for processing segmented point clouds that, through a voting procedure, is able to provide an initial estimate of the geometric parameters characterizing each primitive type. By using these estimates, we localize the search of the optimal solution in a dimensionally-reduced parameter space thus making it efficient to extend the HT to more primitives than those that are generally found in the literature, i.e. planes and spheres. Then, we extract a number of geometric descriptors that uniquely characterize a segment, and, on the basis of these descriptors, we show how to aggregate parts of primitives (segments). Experiments on both synthetic and industrial scans reveal the robustness of the primitive fitting method and its effectiveness for inferring relations among segments.

SHREC 2022: pothole and crack detection in the road pavement using images and RGB-D data

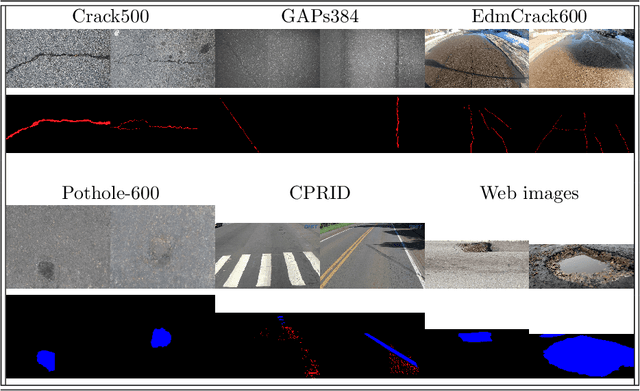
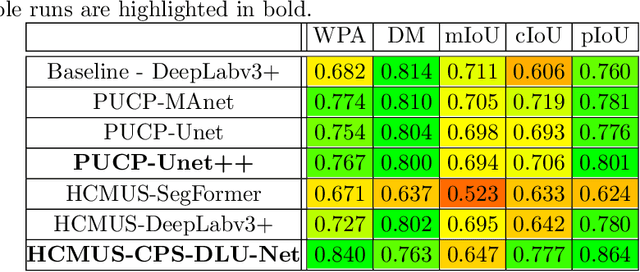
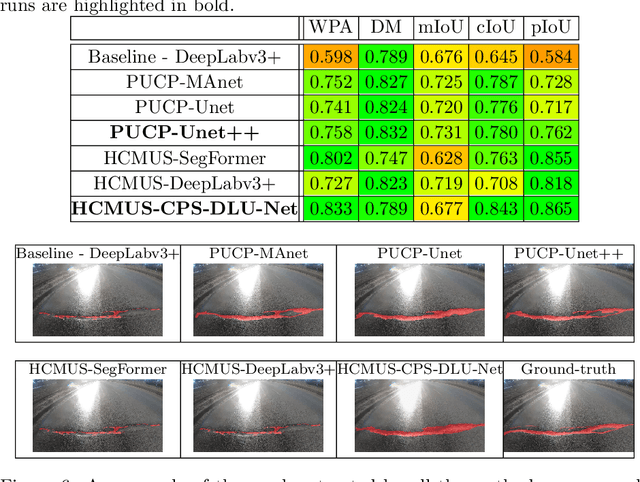
This paper describes the methods submitted for evaluation to the SHREC 2022 track on pothole and crack detection in the road pavement. A total of 7 different runs for the semantic segmentation of the road surface are compared, 6 from the participants plus a baseline method. All methods exploit Deep Learning techniques and their performance is tested using the same environment (i.e.: a single Jupyter notebook). A training set, composed of 3836 semantic segmentation image/mask pairs and 797 RGB-D video clips collected with the latest depth cameras was made available to the participants. The methods are then evaluated on the 496 image/mask pairs in the validation set, on the 504 pairs in the test set and finally on 8 video clips. The analysis of the results is based on quantitative metrics for image segmentation and qualitative analysis of the video clips. The participation and the results show that the scenario is of great interest and that the use of RGB-D data is still challenging in this context.

Edge-based LBP description of surfaces with colorimetric patterns

In this paper we target the problem of the retrieval of colour patterns over surfaces. We generalize to surface tessellations the well known Local Binary Pattern (LBP) descriptor for images. The key concept of the LBP is to code the variability of the colour values around each pixel. In the case of a surface tessellation we adopt rings around vertices that are obtained with a sphere-mesh intersection driven by the edges of the mesh; for this reason, we name our method edgeLBP. Experimental results are provided to show how this description performs well for pattern retrieval, also when patterns come from degraded and corrupted archaeological fragments.

Recognition of feature curves on 3D shapes using an algebraic approach to Hough transforms

Feature curves are largely adopted to highlight shape features, such as sharp lines, or to divide surfaces into meaningful segments, like convex or concave regions. Extracting these curves is not sufficient to convey prominent and meaningful information about a shape. We have first to separate the curves belonging to features from those caused by noise and then to select the lines, which describe non-trivial portions of a surface. The automatic detection of such features is crucial for the identification and/or annotation of relevant parts of a given shape. To do this, the Hough transform (HT) is a feature extraction technique widely used in image analysis, computer vision and digital image processing, while, for 3D shapes, the extraction of salient feature curves is still an open problem. Thanks to algebraic geometry concepts, the HT technique has been recently extended to include a vast class of algebraic curves, thus proving to be a competitive tool for yielding an explicit representation of the diverse feature lines equations. In the paper, for the first time we apply this novel extension of the HT technique to the realm of 3D shapes in order to identify and localize semantic features like patterns, decorations or anatomical details on 3D objects (both complete and fragments), even in the case of features partially damaged or incomplete. The method recognizes various features, possibly compound, and it selects the most suitable feature profiles among families of algebraic curves.