SubZero+: Efficient Zeroth-Order LLM Fine-Tuning via Large Learning Rates

Zeroth-order (ZO) optimization enables backpropagation-free fine-tuning of large language models, but existing ZO methods suffer from high-variance gradient estimators, making convergence unstable and highly sensitive to learning rates. We propose SubZero+, an improved SubZero framework that improves stability in three complementary ways: (i) multi-query gradient estimation within layer-specific low-rank subspaces to reduce variance without exhibiting the multi-query paradox; (ii) a subspace Adam optimizer that performs adaptive updates using in-subspace multi-query gradient statistics; and (iii) a sign correction for QR-based subspace construction to ensure Haar-distributed projection matrices, eliminating implementation-dependent orientation ambiguity. Experiments on models from 1.3B to 32B across SuperGLUE, under both full-parameter tuning and LoRA, show that SubZero+ consistently outperforms prior ZO baselines, enlarges the stable learning-rate range, and narrows the gap to first-order methods with minimal extra memory overhead.

SubZero: Random Subspace Zeroth-Order Optimization for Memory-Efficient LLM Fine-Tuning

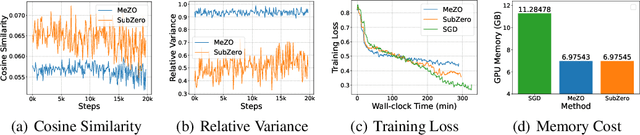
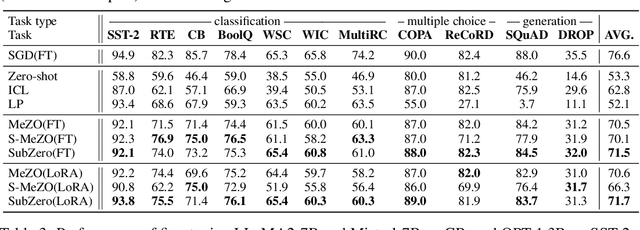
Fine-tuning Large Language Models (LLMs) has proven effective for a variety of downstream tasks. However, as LLMs grow in size, the memory demands for backpropagation become increasingly prohibitive. Zeroth-order (ZO) optimization methods offer a memory-efficient alternative by using forward passes to estimate gradients, but the variance of gradient estimates typically scales linearly with the model's parameter dimension$\unicode{x2013}$a significant issue for LLMs. In this paper, we propose the random Subspace Zeroth-order (SubZero) optimization to address the challenges posed by LLMs' high dimensionality. We introduce a low-rank perturbation tailored for LLMs that significantly reduces memory consumption while improving training performance. Additionally, we prove that our gradient estimation closely approximates the backpropagation gradient, exhibits lower variance than traditional ZO methods, and ensures convergence when combined with SGD. Experimental results show that SubZero enhances fine-tuning performance and achieves faster convergence compared to standard ZO approaches like MeZO across various language modeling tasks.

4-bit Shampoo for Memory-Efficient Network Training

Second-order optimizers, maintaining a matrix termed a preconditioner, are superior to first-order optimizers in both theory and practice. The states forming the preconditioner and its inverse root restrict the maximum size of models trained by second-order optimizers. To address this, compressing 32-bit optimizer states to lower bitwidths has shown promise in reducing memory usage. However, current approaches only pertain to first-order optimizers. In this paper, we propose the first 4-bit second-order optimizers, exemplified by 4-bit Shampoo, maintaining performance similar to that of 32-bit ones. We show that quantizing the eigenvector matrix of the preconditioner in 4-bit Shampoo is remarkably better than quantizing the preconditioner itself both theoretically and experimentally. By rectifying the orthogonality of the quantized eigenvector matrix, we enhance the approximation of the preconditioner's eigenvector matrix, which also benefits the computation of its inverse 4-th root. Besides, we find that linear square quantization slightly outperforms dynamic tree quantization when quantizing second-order optimizer states. Evaluation on various networks for image classification demonstrates that our 4-bit Shampoo achieves comparable test accuracy to its 32-bit counterpart while being more memory-efficient. The source code will be made available.