SubZero: Random Subspace Zeroth-Order Optimization for Memory-Efficient LLM Fine-Tuning
Paper and Code
Oct 11, 2024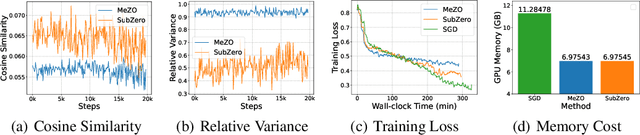

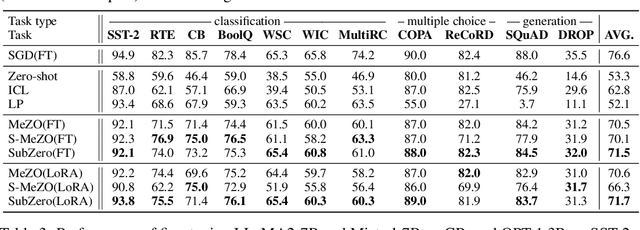

Fine-tuning Large Language Models (LLMs) has proven effective for a variety of downstream tasks. However, as LLMs grow in size, the memory demands for backpropagation become increasingly prohibitive. Zeroth-order (ZO) optimization methods offer a memory-efficient alternative by using forward passes to estimate gradients, but the variance of gradient estimates typically scales linearly with the model's parameter dimension$\unicode{x2013}$a significant issue for LLMs. In this paper, we propose the random Subspace Zeroth-order (SubZero) optimization to address the challenges posed by LLMs' high dimensionality. We introduce a low-rank perturbation tailored for LLMs that significantly reduces memory consumption while improving training performance. Additionally, we prove that our gradient estimation closely approximates the backpropagation gradient, exhibits lower variance than traditional ZO methods, and ensures convergence when combined with SGD. Experimental results show that SubZero enhances fine-tuning performance and achieves faster convergence compared to standard ZO approaches like MeZO across various language modeling tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge