Convolutional Networks for Object Category and 3D Pose Estimation from 2D Images

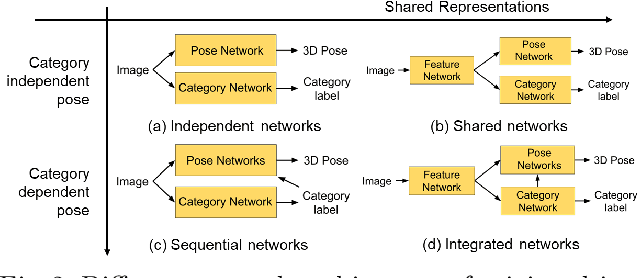
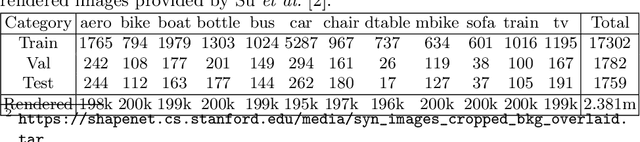
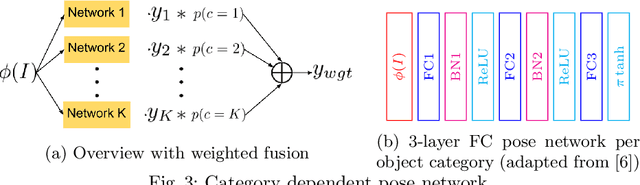
Current CNN-based algorithms for recovering the 3D pose of an object in an image assume knowledge about both the object category and its 2D localization in the image. In this paper, we relax one of these constraints and propose to solve the task of joint object category and 3D pose estimation from an image assuming known 2D localization. We design a new architecture for this task composed of a feature network that is shared between subtasks, an object categorization network built on top of the feature network, and a collection of category dependent pose regression networks. We also introduce suitable loss functions and a training method for the new architecture. Experiments on the challenging PASCAL3D+ dataset show state-of-the-art performance in the joint categorization and pose estimation task. Moreover, our performance on the joint task is comparable to the performance of state-of-the-art methods on the simpler 3D pose estimation with known object category task.

Monocular Object Orientation Estimation using Riemannian Regression and Classification Networks

We consider the task of estimating the 3D orientation of an object of known category given an image of the object and a bounding box around it. Recently, CNN-based regression and classification methods have shown significant performance improvements for this task. This paper proposes a new CNN-based approach to monocular orientation estimation that advances the state of the art in four different directions. First, we take into account the Riemannian structure of the orientation space when designing regression losses and nonlinear activation functions. Second, we propose a mixed Riemannian regression and classification framework that better handles the challenging case of nearly symmetric objects. Third, we propose a data augmentation strategy that is specifically designed to capture changes in 3D orientation. Fourth, our approach leads to state-of-the-art results on the PASCAL3D+ dataset.

A Mixed Classification-Regression Framework for 3D Pose Estimation from 2D Images

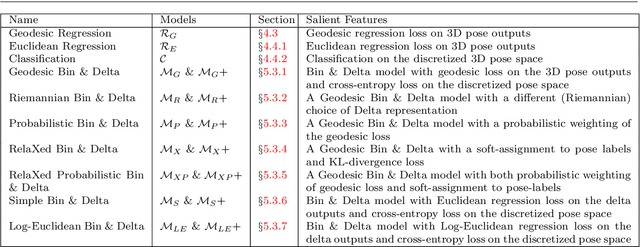
3D pose estimation from a single 2D image is an important and challenging task in computer vision with applications in autonomous driving, robot manipulation and augmented reality. Since 3D pose is a continuous quantity, a natural formulation for this task is to solve a pose regression problem. However, since pose regression methods return a single estimate of the pose, they have difficulties handling multimodal pose distributions (e.g. in the case of symmetric objects). An alternative formulation, which can capture multimodal pose distributions, is to discretize the pose space into bins and solve a pose classification problem. However, pose classification methods can give large pose estimation errors depending on the coarseness of the discretization. In this paper, we propose a mixed classification-regression framework that uses a classification network to produce a discrete multimodal pose estimate and a regression network to produce a continuous refinement of the discrete estimate. The proposed framework can accommodate different architectures and loss functions, leading to multiple classification-regression models, some of which achieve state-of-the-art performance on the challenging Pascal3D+ dataset.

3D Pose Regression using Convolutional Neural Networks

3D pose estimation is a key component of many important computer vision tasks such as autonomous navigation and 3D scene understanding. Most state-of-the-art approaches to 3D pose estimation solve this problem as a pose-classification problem in which the pose space is discretized into bins and a CNN classifier is used to predict a pose bin. We argue that the 3D pose space is continuous and propose to solve the pose estimation problem in a CNN regression framework with a suitable representation, data augmentation and loss function that captures the geometry of the pose space. Experiments on PASCAL3D+ show that the proposed 3D pose regression approach achieves competitive performance compared to the state-of-the-art.

Car Segmentation and Pose Estimation using 3D Object Models

Image segmentation and 3D pose estimation are two key cogs in any algorithm for scene understanding. However, state-of-the-art CRF-based models for image segmentation rely mostly on 2D object models to construct top-down high-order potentials. In this paper, we propose new top-down potentials for image segmentation and pose estimation based on the shape and volume of a 3D object model. We show that these complex top-down potentials can be easily decomposed into standard forms for efficient inference in both the segmentation and pose estimation tasks. Experiments on a car dataset show that knowledge of segmentation helps perform pose estimation better and vice versa.

Hypothesize and Bound: A Computational Focus of Attention Mechanism for Simultaneous 3D Shape Reconstruction, Pose Estimation and Classification from a Single 2D Image

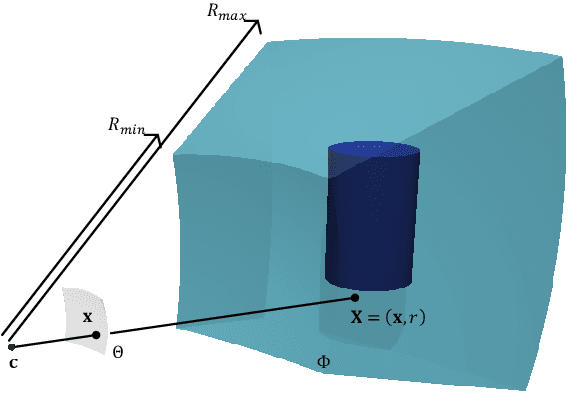
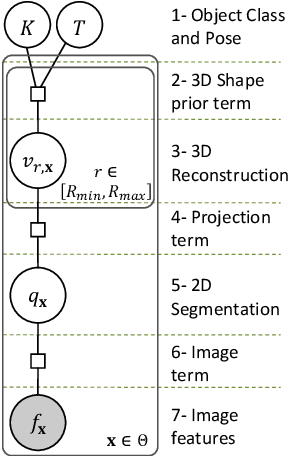
This article presents a mathematical framework to simultaneously tackle the problems of 3D reconstruction, pose estimation and object classification, from a single 2D image. In sharp contrast with state of the art methods that rely primarily on 2D information and solve each of these three problems separately or iteratively, we propose a mathematical framework that incorporates prior "knowledge" about the 3D shapes of different object classes and solves these problems jointly and simultaneously, using a hypothesize-and-bound (H&B) algorithm. In the proposed H&B algorithm one hypothesis is defined for each possible pair [object class, object pose], and the algorithm selects the hypothesis H that maximizes a function L(H) encoding how well each hypothesis "explains" the input image. To find this maximum efficiently, the function L(H) is not evaluated exactly for each hypothesis H, but rather upper and lower bounds for it are computed at a much lower cost. In order to obtain bounds for L(H) that are tight yet inexpensive to compute, we extend the theory of shapes described in [14] to handle projections of shapes. This extension allows us to define a probabilistic relationship between the prior knowledge given in 3D and the 2D input image. This relationship is derived from first principles and is proven to be the only relationship having the properties that we intuitively expect from a "projection." In addition to the efficiency and optimality characteristics of H&B algorithms, the proposed framework has the desirable property of integrating information in the 2D image with information in the 3D prior to estimate the optimal reconstruction. While this article focuses primarily on the problem mentioned above, we believe that the theory presented herein has multiple other potential applications.