Hypothesize and Bound: A Computational Focus of Attention Mechanism for Simultaneous 3D Shape Reconstruction, Pose Estimation and Classification from a Single 2D Image

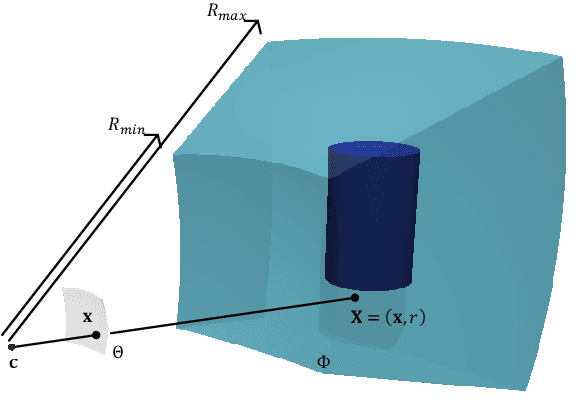
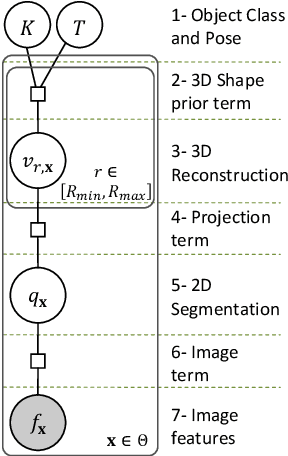
This article presents a mathematical framework to simultaneously tackle the problems of 3D reconstruction, pose estimation and object classification, from a single 2D image. In sharp contrast with state of the art methods that rely primarily on 2D information and solve each of these three problems separately or iteratively, we propose a mathematical framework that incorporates prior "knowledge" about the 3D shapes of different object classes and solves these problems jointly and simultaneously, using a hypothesize-and-bound (H&B) algorithm. In the proposed H&B algorithm one hypothesis is defined for each possible pair [object class, object pose], and the algorithm selects the hypothesis H that maximizes a function L(H) encoding how well each hypothesis "explains" the input image. To find this maximum efficiently, the function L(H) is not evaluated exactly for each hypothesis H, but rather upper and lower bounds for it are computed at a much lower cost. In order to obtain bounds for L(H) that are tight yet inexpensive to compute, we extend the theory of shapes described in [14] to handle projections of shapes. This extension allows us to define a probabilistic relationship between the prior knowledge given in 3D and the 2D input image. This relationship is derived from first principles and is proven to be the only relationship having the properties that we intuitively expect from a "projection." In addition to the efficiency and optimality characteristics of H&B algorithms, the proposed framework has the desirable property of integrating information in the 2D image with information in the 3D prior to estimate the optimal reconstruction. While this article focuses primarily on the problem mentioned above, we believe that the theory presented herein has multiple other potential applications.