Hypothesize and Bound: A Computational Focus of Attention Mechanism for Simultaneous 3D Shape Reconstruction, Pose Estimation and Classification from a Single 2D Image

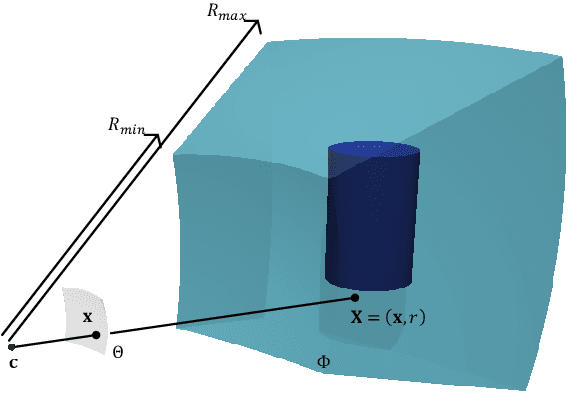
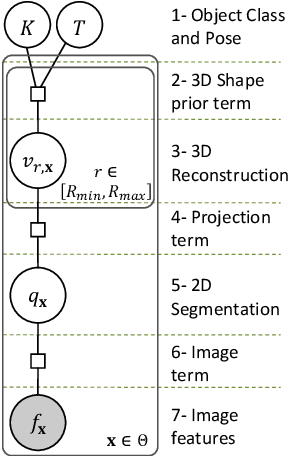
This article presents a mathematical framework to simultaneously tackle the problems of 3D reconstruction, pose estimation and object classification, from a single 2D image. In sharp contrast with state of the art methods that rely primarily on 2D information and solve each of these three problems separately or iteratively, we propose a mathematical framework that incorporates prior "knowledge" about the 3D shapes of different object classes and solves these problems jointly and simultaneously, using a hypothesize-and-bound (H&B) algorithm. In the proposed H&B algorithm one hypothesis is defined for each possible pair [object class, object pose], and the algorithm selects the hypothesis H that maximizes a function L(H) encoding how well each hypothesis "explains" the input image. To find this maximum efficiently, the function L(H) is not evaluated exactly for each hypothesis H, but rather upper and lower bounds for it are computed at a much lower cost. In order to obtain bounds for L(H) that are tight yet inexpensive to compute, we extend the theory of shapes described in [14] to handle projections of shapes. This extension allows us to define a probabilistic relationship between the prior knowledge given in 3D and the 2D input image. This relationship is derived from first principles and is proven to be the only relationship having the properties that we intuitively expect from a "projection." In addition to the efficiency and optimality characteristics of H&B algorithms, the proposed framework has the desirable property of integrating information in the 2D image with information in the 3D prior to estimate the optimal reconstruction. While this article focuses primarily on the problem mentioned above, we believe that the theory presented herein has multiple other potential applications.

Hypothesize and Bound: A Computational Focus of Attention Mechanism for Simultaneous N-D Segmentation, Pose Estimation and Classification Using Shape Priors

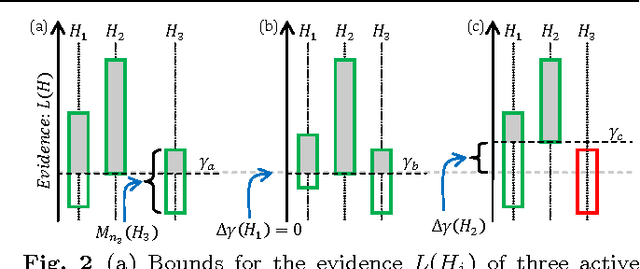
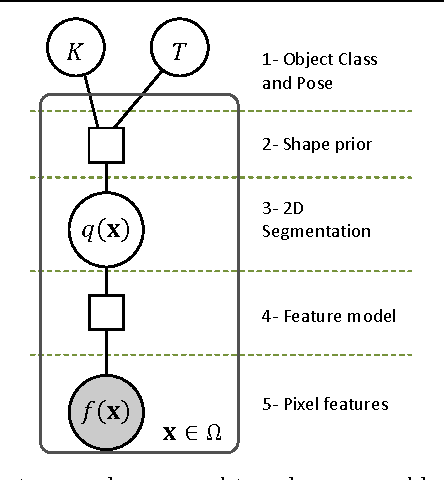
Given the ever increasing bandwidth of the visual information available to many intelligent systems, it is becoming essential to endow them with a sense of what is worthwhile their attention and what can be safely disregarded. This article presents a general mathematical framework to efficiently allocate the available computational resources to process the parts of the input that are relevant to solve a given perceptual problem. By this we mean to find the hypothesis H (i.e., the state of the world) that maximizes a function L(H), representing how well each hypothesis "explains" the input. Given the large bandwidth of the sensory input, fully evaluating L(H) for each hypothesis H is computationally infeasible (e.g., because it would imply checking a large number of pixels). To address this problem we propose a mathematical framework with two key ingredients. The first one is a Bounding Mechanism (BM) to compute lower and upper bounds of L(H), for a given computational budget. These bounds are much cheaper to compute than L(H) itself, can be refined at any time by increasing the budget allocated to a hypothesis, and are frequently enough to discard a hypothesis. To compute these bounds, we develop a novel theory of shapes and shape priors. The second ingredient is a Focus of Attention Mechanism (FoAM) to select which hypothesis' bounds should be refined next, with the goal of discarding non-optimal hypotheses with the least amount of computation. The proposed framework: 1) is very efficient since most hypotheses are discarded with minimal computation; 2) is parallelizable; 3) is guaranteed to find the globally optimal hypothesis; and 4) its running time depends on the problem at hand, not on the bandwidth of the input. We instantiate the proposed framework for the problem of simultaneously estimating the class, pose, and a noiseless version of a 2D shape in a 2D image.