Hypothesize and Bound: A Computational Focus of Attention Mechanism for Simultaneous N-D Segmentation, Pose Estimation and Classification Using Shape Priors

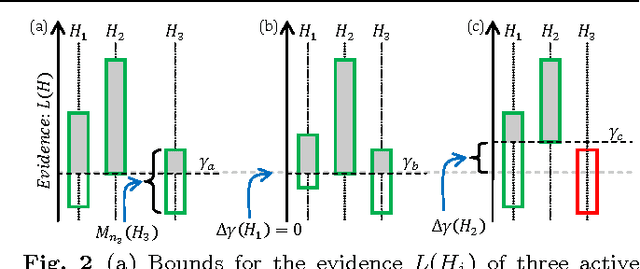
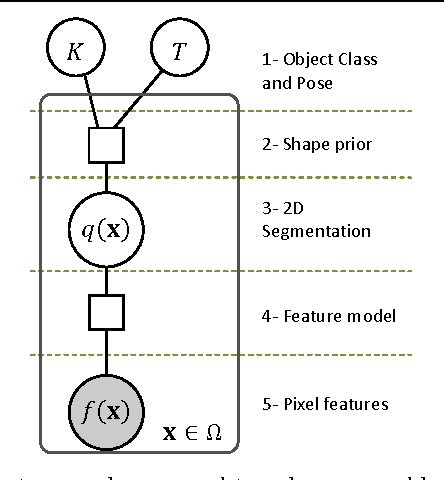
Given the ever increasing bandwidth of the visual information available to many intelligent systems, it is becoming essential to endow them with a sense of what is worthwhile their attention and what can be safely disregarded. This article presents a general mathematical framework to efficiently allocate the available computational resources to process the parts of the input that are relevant to solve a given perceptual problem. By this we mean to find the hypothesis H (i.e., the state of the world) that maximizes a function L(H), representing how well each hypothesis "explains" the input. Given the large bandwidth of the sensory input, fully evaluating L(H) for each hypothesis H is computationally infeasible (e.g., because it would imply checking a large number of pixels). To address this problem we propose a mathematical framework with two key ingredients. The first one is a Bounding Mechanism (BM) to compute lower and upper bounds of L(H), for a given computational budget. These bounds are much cheaper to compute than L(H) itself, can be refined at any time by increasing the budget allocated to a hypothesis, and are frequently enough to discard a hypothesis. To compute these bounds, we develop a novel theory of shapes and shape priors. The second ingredient is a Focus of Attention Mechanism (FoAM) to select which hypothesis' bounds should be refined next, with the goal of discarding non-optimal hypotheses with the least amount of computation. The proposed framework: 1) is very efficient since most hypotheses are discarded with minimal computation; 2) is parallelizable; 3) is guaranteed to find the globally optimal hypothesis; and 4) its running time depends on the problem at hand, not on the bandwidth of the input. We instantiate the proposed framework for the problem of simultaneously estimating the class, pose, and a noiseless version of a 2D shape in a 2D image.