Learning a Fuzzy Hyperplane Fat Margin Classifier with Minimum VC dimension

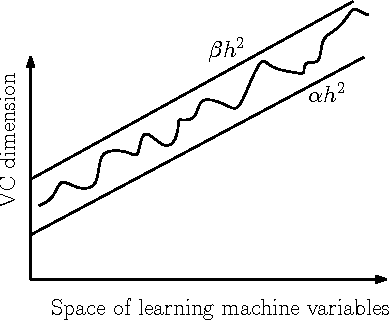
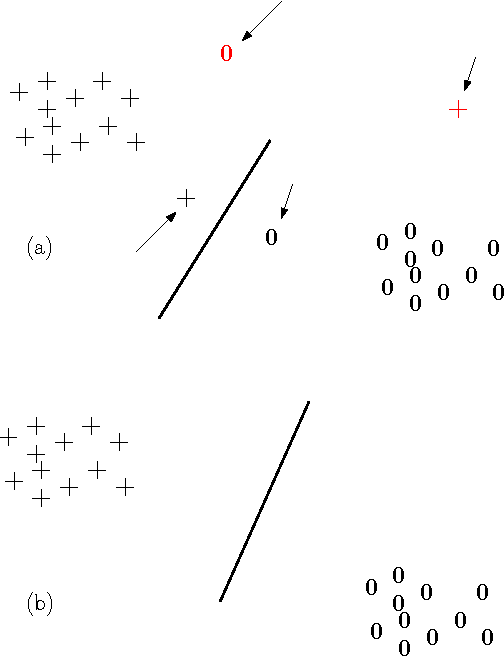
The Vapnik-Chervonenkis (VC) dimension measures the complexity of a learning machine, and a low VC dimension leads to good generalization. The recently proposed Minimal Complexity Machine (MCM) learns a hyperplane classifier by minimizing an exact bound on the VC dimension. This paper extends the MCM classifier to the fuzzy domain. The use of a fuzzy membership is known to reduce the effect of outliers, and to reduce the effect of noise on learning. Experimental results show, that on a number of benchmark datasets, the the fuzzy MCM classifier outperforms SVMs and the conventional MCM in terms of generalization, and that the fuzzy MCM uses fewer support vectors. On several benchmark datasets, the fuzzy MCM classifier yields excellent test set accuracies while using one-tenth the number of support vectors used by SVMs.

Learning a hyperplane regressor by minimizing an exact bound on the VC dimension

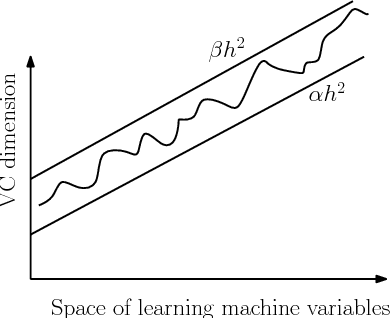
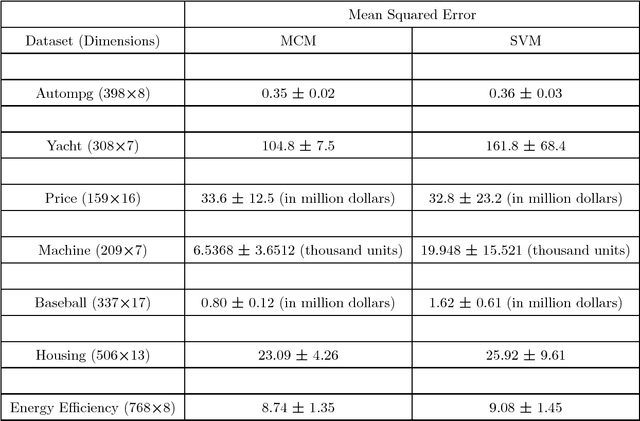
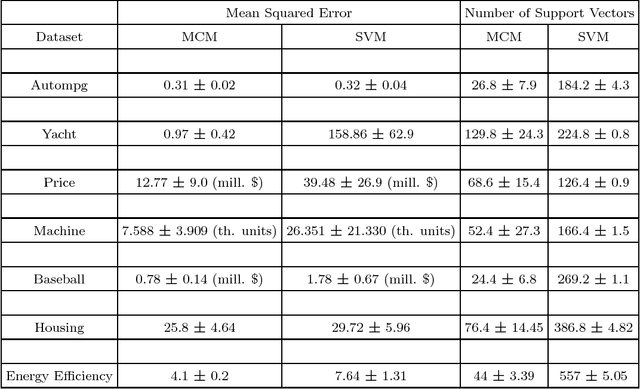
The capacity of a learning machine is measured by its Vapnik-Chervonenkis dimension, and learning machines with a low VC dimension generalize better. It is well known that the VC dimension of SVMs can be very large or unbounded, even though they generally yield state-of-the-art learning performance. In this paper, we show how to learn a hyperplane regressor by minimizing an exact, or \boldmath{$\Theta$} bound on its VC dimension. The proposed approach, termed as the Minimal Complexity Machine (MCM) Regressor, involves solving a simple linear programming problem. Experimental results show, that on a number of benchmark datasets, the proposed approach yields regressors with error rates much less than those obtained with conventional SVM regresssors, while often using fewer support vectors. On some benchmark datasets, the number of support vectors is less than one tenth the number used by SVMs, indicating that the MCM does indeed learn simpler representations.