Learning a Fuzzy Hyperplane Fat Margin Classifier with Minimum VC dimension
Paper and Code
Jan 11, 2015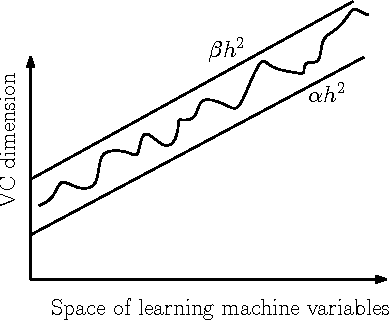

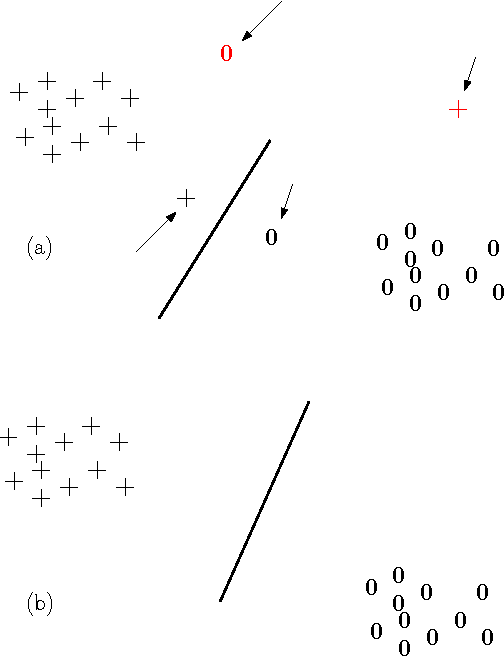

The Vapnik-Chervonenkis (VC) dimension measures the complexity of a learning machine, and a low VC dimension leads to good generalization. The recently proposed Minimal Complexity Machine (MCM) learns a hyperplane classifier by minimizing an exact bound on the VC dimension. This paper extends the MCM classifier to the fuzzy domain. The use of a fuzzy membership is known to reduce the effect of outliers, and to reduce the effect of noise on learning. Experimental results show, that on a number of benchmark datasets, the the fuzzy MCM classifier outperforms SVMs and the conventional MCM in terms of generalization, and that the fuzzy MCM uses fewer support vectors. On several benchmark datasets, the fuzzy MCM classifier yields excellent test set accuracies while using one-tenth the number of support vectors used by SVMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge