Feature Selection through Minimization of the VC dimension

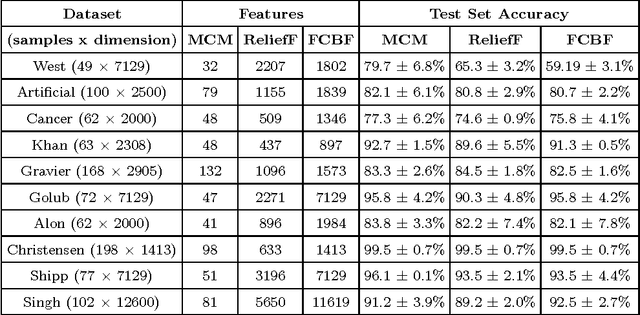
Feature selection involes identifying the most relevant subset of input features, with a view to improving generalization of predictive models by reducing overfitting. Directly searching for the most relevant combination of attributes is NP-hard. Variable selection is of critical importance in many applications, such as micro-array data analysis, where selecting a small number of discriminative features is crucial to developing useful models of disease mechanisms, as well as for prioritizing targets for drug discovery. The recently proposed Minimal Complexity Machine (MCM) provides a way to learn a hyperplane classifier by minimizing an exact (\boldmath{$\Theta$}) bound on its VC dimension. It is well known that a lower VC dimension contributes to good generalization. For a linear hyperplane classifier in the input space, the VC dimension is upper bounded by the number of features; hence, a linear classifier with a small VC dimension is parsimonious in the set of features it employs. In this paper, we use the linear MCM to learn a classifier in which a large number of weights are zero; features with non-zero weights are the ones that are chosen. Selected features are used to learn a kernel SVM classifier. On a number of benchmark datasets, the features chosen by the linear MCM yield comparable or better test set accuracy than when methods such as ReliefF and FCBF are used for the task. The linear MCM typically chooses one-tenth the number of attributes chosen by the other methods; on some very high dimensional datasets, the MCM chooses about $0.6\%$ of the features; in comparison, ReliefF and FCBF choose 70 to 140 times more features, thus demonstrating that minimizing the VC dimension may provide a new, and very effective route for feature selection and for learning sparse representations.

Learning a hyperplane regressor by minimizing an exact bound on the VC dimension

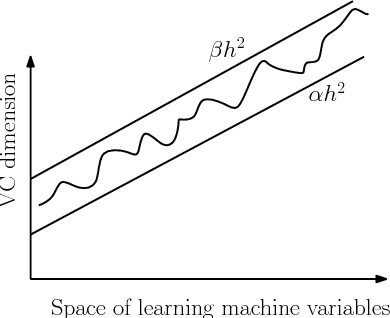
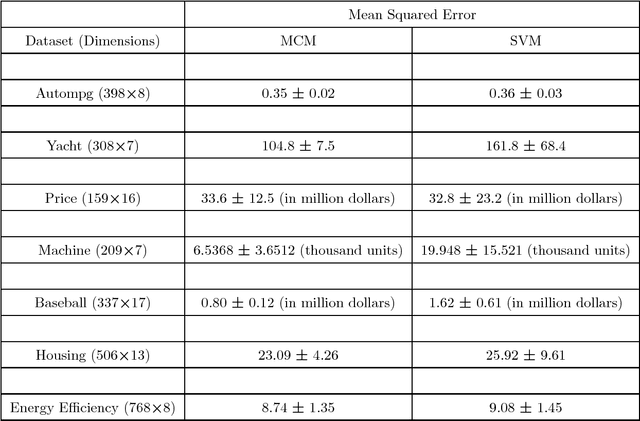
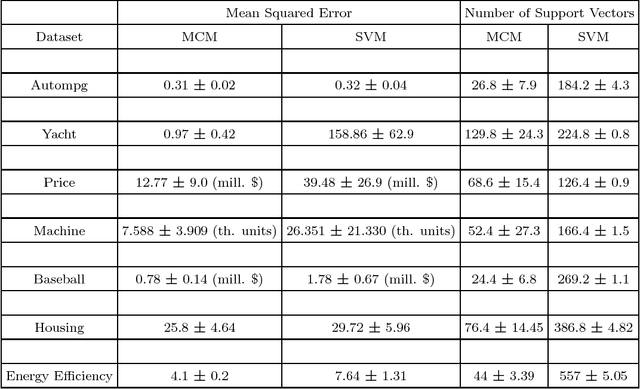
The capacity of a learning machine is measured by its Vapnik-Chervonenkis dimension, and learning machines with a low VC dimension generalize better. It is well known that the VC dimension of SVMs can be very large or unbounded, even though they generally yield state-of-the-art learning performance. In this paper, we show how to learn a hyperplane regressor by minimizing an exact, or \boldmath{$\Theta$} bound on its VC dimension. The proposed approach, termed as the Minimal Complexity Machine (MCM) Regressor, involves solving a simple linear programming problem. Experimental results show, that on a number of benchmark datasets, the proposed approach yields regressors with error rates much less than those obtained with conventional SVM regresssors, while often using fewer support vectors. On some benchmark datasets, the number of support vectors is less than one tenth the number used by SVMs, indicating that the MCM does indeed learn simpler representations.