OTAD: An Optimal Transport-Induced Robust Model for Agnostic Adversarial Attack

Deep neural networks (DNNs) are vulnerable to small adversarial perturbations of the inputs, posing a significant challenge to their reliability and robustness. Empirical methods such as adversarial training can defend against particular attacks but remain vulnerable to more powerful attacks. Alternatively, Lipschitz networks provide certified robustness to unseen perturbations but lack sufficient expressive power. To harness the advantages of both approaches, we design a novel two-step Optimal Transport induced Adversarial Defense (OTAD) model that can fit the training data accurately while preserving the local Lipschitz continuity. First, we train a DNN with a regularizer derived from optimal transport theory, yielding a discrete optimal transport map linking data to its features. By leveraging the map's inherent regularity, we interpolate the map by solving the convex integration problem (CIP) to guarantee the local Lipschitz property. OTAD is extensible to diverse architectures of ResNet and Transformer, making it suitable for complex data. For efficient computation, the CIP can be solved through training neural networks. OTAD opens a novel avenue for developing reliable and secure deep learning systems through the regularity of optimal transport maps. Empirical results demonstrate that OTAD can outperform other robust models on diverse datasets.

Progressive Feedforward Collapse of ResNet Training

Neural collapse (NC) is a simple and symmetric phenomenon for deep neural networks (DNNs) at the terminal phase of training, where the last-layer features collapse to their class means and form a simplex equiangular tight frame aligning with the classifier vectors. However, the relationship of the last-layer features to the data and intermediate layers during training remains unexplored. To this end, we characterize the geometry of intermediate layers of ResNet and propose a novel conjecture, progressive feedforward collapse (PFC), claiming the degree of collapse increases during the forward propagation of DNNs. We derive a transparent model for the well-trained ResNet according to that ResNet with weight decay approximates the geodesic curve in Wasserstein space at the terminal phase. The metrics of PFC indeed monotonically decrease across depth on various datasets. We propose a new surrogate model, multilayer unconstrained feature model (MUFM), connecting intermediate layers by an optimal transport regularizer. The optimal solution of MUFM is inconsistent with NC but is more concentrated relative to the input data. Overall, this study extends NC to PFC to model the collapse phenomenon of intermediate layers and its dependence on the input data, shedding light on the theoretical understanding of ResNet in classification problems.

Privacy-Preserving Spam Filtering using Functional Encryption

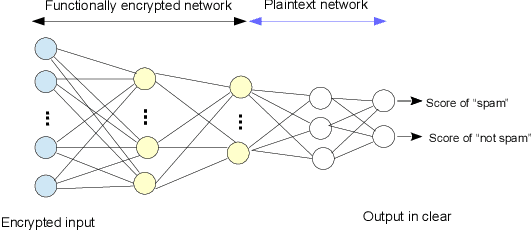
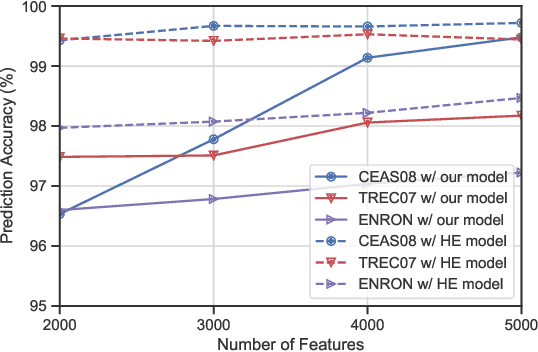
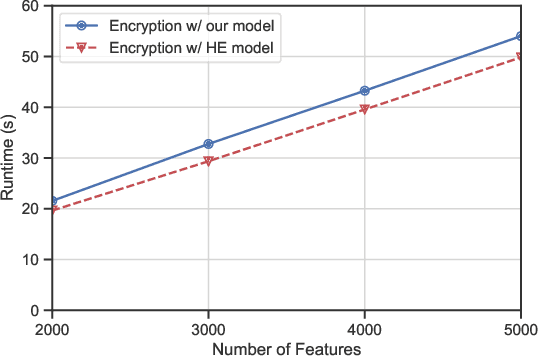
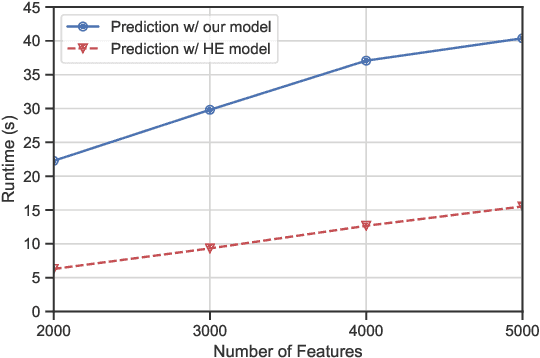
Traditional spam classification requires the end-user to reveal the content of its received email to the spam classifier which violates the privacy. Spam classification over encrypted emails enables the classifier to classify spam email without accessing the email, hence protects the privacy of email content. In this paper, we construct a spam classification framework that enables the classification of encrypted emails. Our classification model is based on a neural network with a quadratic network part and a multi-layer perception network part. The quadratic network architecture is compatible with the operation of an existing quadratic functional encryption scheme that enables our classification to predict the label of encrypted emails without revealing the associated plain-text email. The evaluation results on real-world spam datasets indicate that our proposed spam classification model achieves an accuracy of over 96%.