OTAD: An Optimal Transport-Induced Robust Model for Agnostic Adversarial Attack

Deep neural networks (DNNs) are vulnerable to small adversarial perturbations of the inputs, posing a significant challenge to their reliability and robustness. Empirical methods such as adversarial training can defend against particular attacks but remain vulnerable to more powerful attacks. Alternatively, Lipschitz networks provide certified robustness to unseen perturbations but lack sufficient expressive power. To harness the advantages of both approaches, we design a novel two-step Optimal Transport induced Adversarial Defense (OTAD) model that can fit the training data accurately while preserving the local Lipschitz continuity. First, we train a DNN with a regularizer derived from optimal transport theory, yielding a discrete optimal transport map linking data to its features. By leveraging the map's inherent regularity, we interpolate the map by solving the convex integration problem (CIP) to guarantee the local Lipschitz property. OTAD is extensible to diverse architectures of ResNet and Transformer, making it suitable for complex data. For efficient computation, the CIP can be solved through training neural networks. OTAD opens a novel avenue for developing reliable and secure deep learning systems through the regularity of optimal transport maps. Empirical results demonstrate that OTAD can outperform other robust models on diverse datasets.

Analytical Solution of a Three-layer Network with a Matrix Exponential Activation Function

In practice, deeper networks tend to be more powerful than shallow ones, but this has not been understood theoretically. In this paper, we find the analytical solution of a three-layer network with a matrix exponential activation function, i.e., $$ f(X)=W_3\exp(W_2\exp(W_1X)), X\in \mathbb{C}^{d\times d} $$ have analytical solutions for the equations $$ Y_1=f(X_1),Y_2=f(X_2) $$ for $X_1,X_2,Y_1,Y_2$ with only invertible assumptions. Our proof shows the power of depth and the use of a non-linear activation function, since one layer network can only solve one equation,i.e.,$Y=WX$.

Progressive Feedforward Collapse of ResNet Training

Neural collapse (NC) is a simple and symmetric phenomenon for deep neural networks (DNNs) at the terminal phase of training, where the last-layer features collapse to their class means and form a simplex equiangular tight frame aligning with the classifier vectors. However, the relationship of the last-layer features to the data and intermediate layers during training remains unexplored. To this end, we characterize the geometry of intermediate layers of ResNet and propose a novel conjecture, progressive feedforward collapse (PFC), claiming the degree of collapse increases during the forward propagation of DNNs. We derive a transparent model for the well-trained ResNet according to that ResNet with weight decay approximates the geodesic curve in Wasserstein space at the terminal phase. The metrics of PFC indeed monotonically decrease across depth on various datasets. We propose a new surrogate model, multilayer unconstrained feature model (MUFM), connecting intermediate layers by an optimal transport regularizer. The optimal solution of MUFM is inconsistent with NC but is more concentrated relative to the input data. Overall, this study extends NC to PFC to model the collapse phenomenon of intermediate layers and its dependence on the input data, shedding light on the theoretical understanding of ResNet in classification problems.

A Mathematical Principle of Deep Learning: Learn the Geodesic Curve in the Wasserstein Space

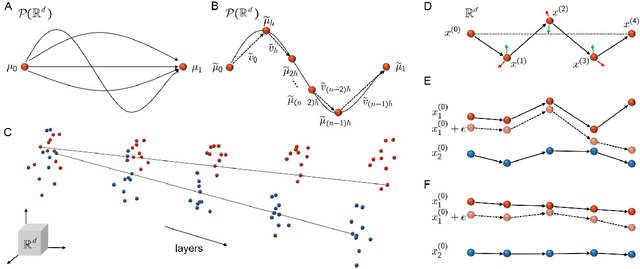
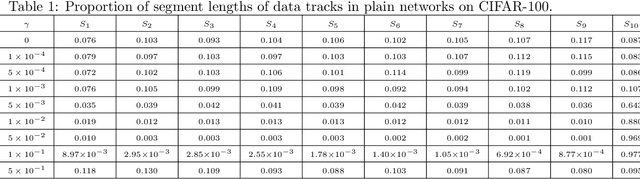
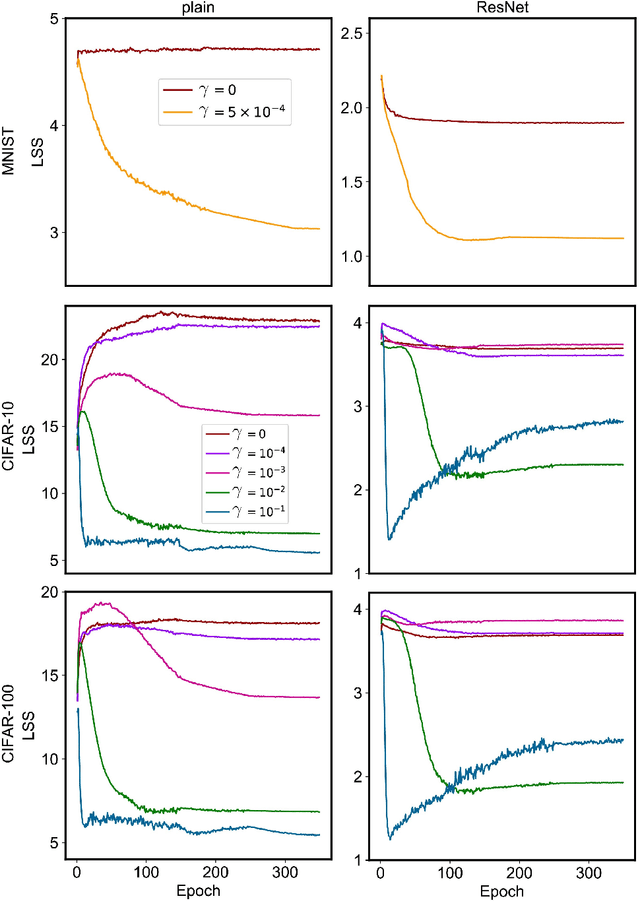
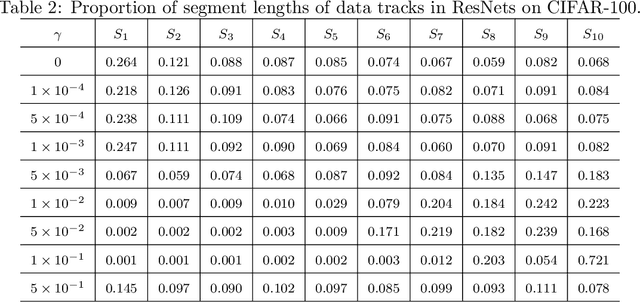
Recent studies revealed the mathematical connection of deep neural network (DNN) and dynamic system. However, the fundamental principle of DNN has not been fully characterized with dynamic system in terms of optimization and generalization. To this end, we build the connection of DNN and continuity equation where the measure is conserved to model the forward propagation process of DNN which has not been addressed before. DNN learns the transformation of the input distribution to the output one. However, in the measure space, there are infinite curves connecting two distributions. Which one can lead to good optimization and generaliztion for DNN? By diving the optimal transport theory, we find DNN with weight decay attempts to learn the geodesic curve in the Wasserstein space, which is induced by the optimal transport map. Compared with plain network, ResNet is a better approximation to the geodesic curve, which explains why ResNet can be optimized and generalize better. Numerical experiments show that the data tracks of both plain network and ResNet tend to be line-shape in term of line-shape score (LSS), and the map learned by ResNet is closer to the optimal transport map in term of optimal transport score (OTS). In a word, we conclude a mathematical principle of deep learning is to learn the geodesic curve in the Wasserstein space; and deep learning is a great engineering realization of continuous transformation in high-dimensional space.

Tessellated Wasserstein Auto-Encoders

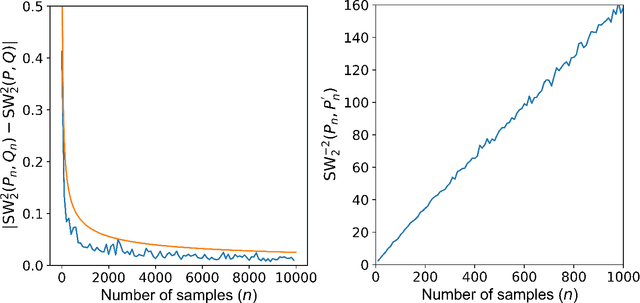
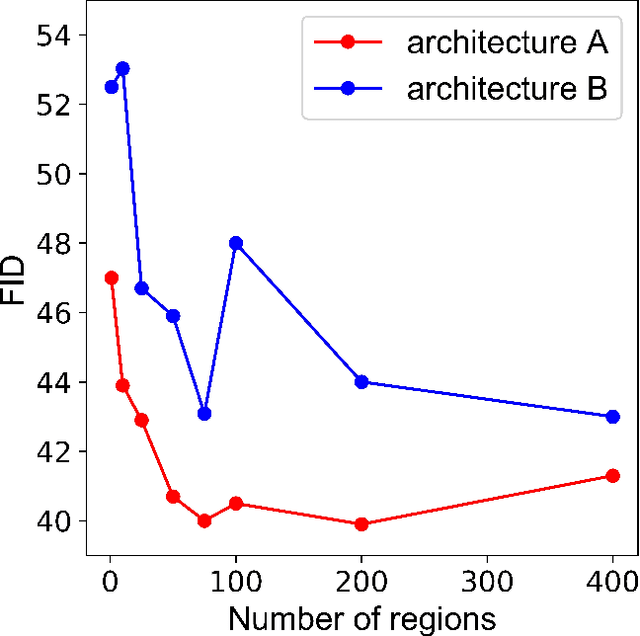
Non-adversarial generative models such as variational auto-encoder (VAE), Wasserstein auto-encoders with maximum mean discrepancy (WAE-MMD), sliced-Wasserstein auto-encoder (SWAE) are relatively easy to train and have less mode collapse compared to Wasserstein auto-encoder with generative adversarial network (WAE-GAN). However, they are not very accurate in approximating the target distribution in the latent space because they don't have a discriminator to detect the minor difference between real and fake. To this end, we develop a novel non-adversarial framework called Tessellated Wasserstein Auto-encoders (TWAE) to tessellate the support of the target distribution into a given number of regions by the centroidal Voronoi tessellation (CVT) technique and design batches of data according to the tessellation instead of random shuffling for accurate computation of discrepancy. Theoretically, we demonstrate that the error of estimate to the discrepancy decreases when the numbers of samples $n$ and regions $m$ of the tessellation become larger with rates of $\mathcal{O}(\frac{1}{\sqrt{n}})$ and $\mathcal{O}(\frac{1}{\sqrt{m}})$, respectively. Given fixed $n$ and $m$, a necessary condition for the upper bound of measurement error to be minimized is that the tessellation is the one determined by CVT. TWAE is very flexible to different non-adversarial metrics and can substantially enhance their generative performance in terms of Fr\'{e}chet inception distance (FID) compared to VAE, WAE-MMD, SWAE. Moreover, numerical results indeed demonstrate that TWAE is competitive to the adversarial model WAE-GAN, demonstrating its powerful generative ability.

Matrix Normal PCA for Interpretable Dimension Reduction and Graphical Noise Modeling

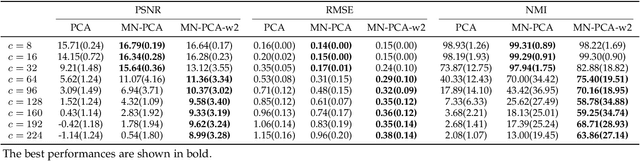
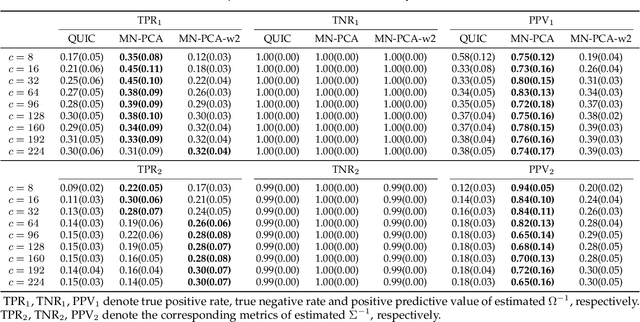
Principal component analysis (PCA) is one of the most widely used dimension reduction and multivariate statistical techniques. From a probabilistic perspective, PCA seeks a low-dimensional representation of data in the presence of independent identical Gaussian noise. Probabilistic PCA (PPCA) and its variants have been extensively studied for decades. Most of them assume the underlying noise follows a certain independent identical distribution. However, the noise in the real world is usually complicated and structured. To address this challenge, some non-linear variants of PPCA have been proposed. But those methods are generally difficult to interpret. To this end, we propose a powerful and intuitive PCA method (MN-PCA) through modeling the graphical noise by the matrix normal distribution, which enables us to explore the structure of noise in both the feature space and the sample space. MN-PCA obtains a low-rank representation of data and the structure of noise simultaneously. And it can be explained as approximating data over the generalized Mahalanobis distance. We develop two algorithms to solve this model: one maximizes the regularized likelihood, the other exploits the Wasserstein distance, which is more robust. Extensive experiments on various data demonstrate their effectiveness.