Matrix Normal PCA for Interpretable Dimension Reduction and Graphical Noise Modeling

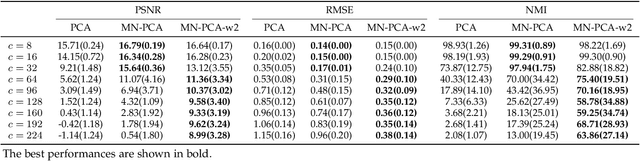
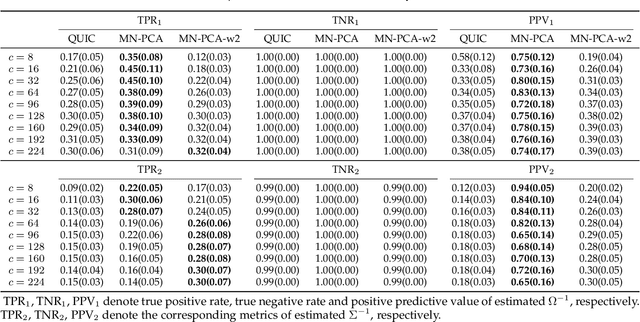
Principal component analysis (PCA) is one of the most widely used dimension reduction and multivariate statistical techniques. From a probabilistic perspective, PCA seeks a low-dimensional representation of data in the presence of independent identical Gaussian noise. Probabilistic PCA (PPCA) and its variants have been extensively studied for decades. Most of them assume the underlying noise follows a certain independent identical distribution. However, the noise in the real world is usually complicated and structured. To address this challenge, some non-linear variants of PPCA have been proposed. But those methods are generally difficult to interpret. To this end, we propose a powerful and intuitive PCA method (MN-PCA) through modeling the graphical noise by the matrix normal distribution, which enables us to explore the structure of noise in both the feature space and the sample space. MN-PCA obtains a low-rank representation of data and the structure of noise simultaneously. And it can be explained as approximating data over the generalized Mahalanobis distance. We develop two algorithms to solve this model: one maximizes the regularized likelihood, the other exploits the Wasserstein distance, which is more robust. Extensive experiments on various data demonstrate their effectiveness.