Exact Recovery of Community Detection in dependent Gaussian Mixture Models

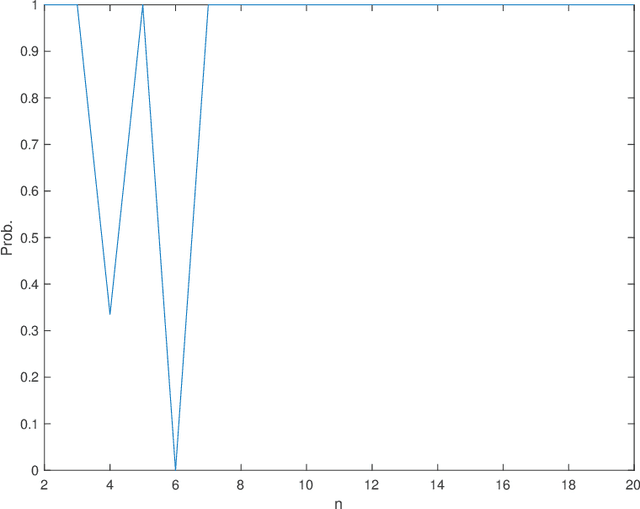
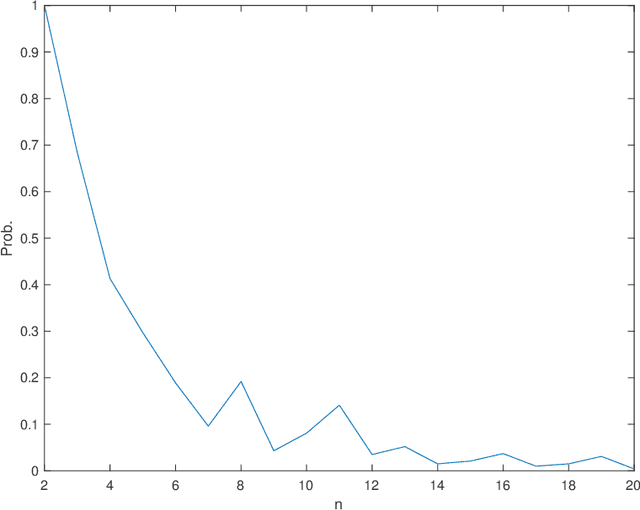
We study the community detection problem on a Gaussian mixture model, in which (1) vertices are divided into $k\geq 2$ distinct communities that are not necessarily equally-sized; (2) the Gaussian perturbations for different entries in the observation matrix are not necessarily independent or identically distributed. We prove necessary and sufficient conditions for the exact recovery of the maximum likelihood estimation (MLE), and discuss the cases when these necessary and sufficient conditions give sharp threshold. Applications include the community detection on a graph where the Gaussian perturbations of observations on each edge is the sum of i.i.d.~Gaussian random variables on its end vertices, in which we explicitly obtain the threshold for the exact recovery of the MLE.

Nonlinear model reduction for slow-fast stochastic systems near manifolds

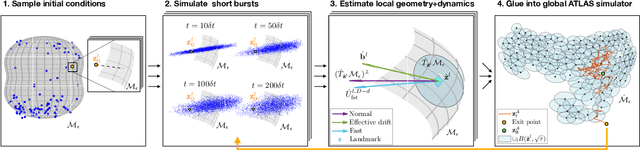
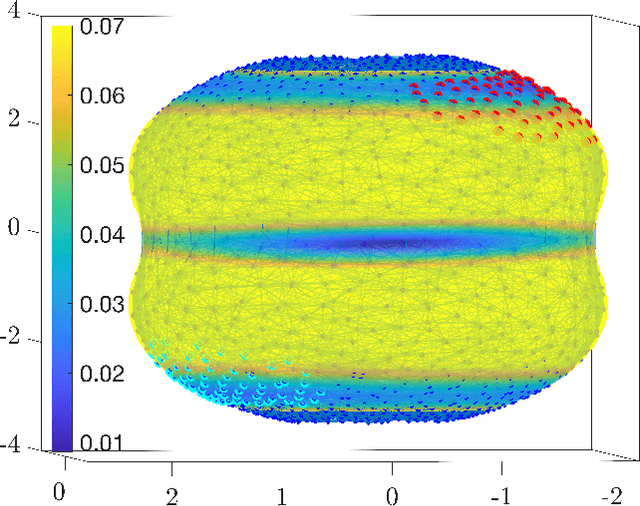
We introduce a nonlinear stochastic model reduction technique for high-dimensional stochastic dynamical systems that have a low-dimensional invariant effective manifold with slow dynamics, and high-dimensional, large fast modes. Given only access to a black box simulator from which short bursts of simulation can be obtained, we estimate the invariant manifold, a process of the effective (stochastic) dynamics on it, and construct an efficient simulator thereof. These estimation steps can be performed on-the-fly, leading to efficient exploration of the effective state space, without losing consistency with the underlying dynamics. This construction enables fast and efficient simulation of paths of the effective dynamics, together with estimation of crucial features and observables of such dynamics, including the stationary distribution, identification of metastable states, and residence times and transition rates between them.

Image Super-Resolution Using a Wavelet-based Generative Adversarial Network

In this paper, we consider the problem of super-resolution recons-truction. This is a hot topic because super-resolution reconstruction has a wide range of applications in the medical field, remote sensing monitoring, and criminal investigation. Compared with traditional algorithms, the current super-resolution reconstruction algorithm based on deep learning greatly improves the clarity of reconstructed pictures. Existing work like Super-Resolution Using a Generative Adversarial Network (SRGAN) can effectively restore the texture details of the image. However, experimentally verified that the texture details of the image recovered by the SRGAN are not robust. In order to get super-resolution reconstructed images with richer high-frequency details, we improve the network structure and propose a super-resolution reconstruction algorithm combining wavelet transform and Generative Adversarial Network. The proposed algorithm can efficiently reconstruct high-resolution images with rich global information and local texture details. We have trained our model by PyTorch framework and VOC2012 dataset, and tested it by Set5, Set14, BSD100 and Urban100 test datasets.